题目内容
20.定义域为R的函数f(x)满足:对任意的m,n∈R有f(m+n)=f(m)•f(n),且当x>0时,有0<f(x)<1,f(4)=$\frac{1}{16}$(1)证明:f(x)>0在R上恒成立;
(2)证明:f(x)在R上是减函数;
(3)若x>0时,不等式4f(x)f(ax)>f(x2)恒成立,求实数a的取值范围.
分析 (1)利用赋值法,令m=2,n=0,求得f(0)的值,令x<0,且y=-x,则-x>0,f(-x)>1,得到0<f(x)<1,问题得以证明.
(2)利用函数单调性的定义进行证明;
(3)利用函数的单调性化为具体不等式,再分离参数,即可求实数a的取值范围.
解答 (1)证明:①令m=2,n=0,可得f(0+2)=f(0)f(2),∴f(0)=1
②令x<0,且y=-x,则-x>0,f(-x)>1,
∴f(x-x)=f(x)•f(-x)=1,
∵f(-x)>1,
∴0<f(x)<1,
综上所述,f(x)>0在R上恒成立.…(4分)
(2)证明:任取实数x1,x2,∈(-∞,+∞),且x1<x2,
则有x2-x1>0,从而可得0<f(x2-x1)<1
又∵f(x2)=f[x1+(x2-x1)]=f(x1)f(x2-x1)<f(x1)
∴f(x)在R上是减函数…(7分)
(3)令m=n=2可得f(2+2)=f(2)f(2)=$\frac{1}{16}$,
∴f(2)=$\frac{1}{4}$
∴4f(x)f(ax)>f(x2)可化为f(x)f(ax)>f(2)f(x2)
∴f(x+ax)>f(2+x2)
∴x+ax<2+x2,
从而当x>0时,有a+1<$\frac{2+{x}^{2}}{x}$恒成立.
令h(x)=$\frac{2+{x}^{2}}{x}$=x+$\frac{2}{x}$≥2$\sqrt{2}$,从而可得a<2$\sqrt{2}$-1…(12分)
点评 本题主要考查了抽象函数表达式反映函数性质及抽象函数表达式的应用,关键是转化化归的思想的应用,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
5.已知对数函数f(x)过点(2,4),则f($\root{4}{2}$)的值为( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
 的方程
的方程 有解,则实数
有解,则实数 的取值范围是( )
的取值范围是( )



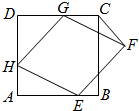 已知,如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD边AB,CD,DA上,AH=2,连接CF.
已知,如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E,G,H分别在正方形ABCD边AB,CD,DA上,AH=2,连接CF.