题目内容
酒杯的形状为倒立的圆锥,杯深8cm,上口宽6cm,水以20cm3/s的流量倒入杯中,当水深为4cm时,则水面升高的瞬时变化率是 .
【答案】分析:作出如图的图象,建立起水面高h与时间t的函数关系,利用导数求出水面升高时的瞬时变化率即得到正确答案
解答: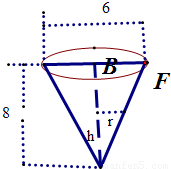 解:由题意,如图,设t时刻水面高为h,水面圆半径是r,
解:由题意,如图,设t时刻水面高为h,水面圆半径是r,
由图知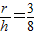 可得r=
可得r= h,此时水的体积为
h,此时水的体积为 ×π×r2×h=
×π×r2×h=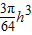
又由题设条件知,此时的水量为20t
故有20t=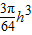 ,故有h=
,故有h=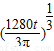
h'= ×
×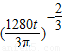 ×
×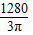
又当h=4时,有t=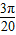 ,故h=4时,h'=
,故h=4时,h'= ×
×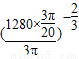 ×
×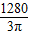 =
=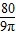
当水深为4cm时,则水面升高的瞬时变化率是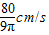
故答案为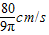
点评:本题考查变化的快慢与变化率,正确解答本题关键是得出高度关于时间的函数关系,然后利用导数求出高度为4时刻的导数值,即得出此时的变化率,本题是一个应用题求解此类题,正确理解题意很关键.由于所得的解析式复杂,解题时运算量较大,要认真解题避免因为运算出错导致解题失败.
解答:
 解:由题意,如图,设t时刻水面高为h,水面圆半径是r,
解:由题意,如图,设t时刻水面高为h,水面圆半径是r,由图知
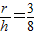 可得r=
可得r= h,此时水的体积为
h,此时水的体积为 ×π×r2×h=
×π×r2×h=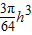
又由题设条件知,此时的水量为20t
故有20t=
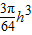 ,故有h=
,故有h=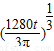
h'=
 ×
×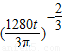 ×
×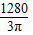
又当h=4时,有t=
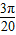 ,故h=4时,h'=
,故h=4时,h'= ×
×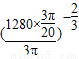 ×
×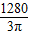 =
=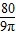
当水深为4cm时,则水面升高的瞬时变化率是
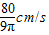
故答案为
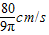
点评:本题考查变化的快慢与变化率,正确解答本题关键是得出高度关于时间的函数关系,然后利用导数求出高度为4时刻的导数值,即得出此时的变化率,本题是一个应用题求解此类题,正确理解题意很关键.由于所得的解析式复杂,解题时运算量较大,要认真解题避免因为运算出错导致解题失败.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
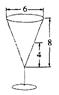
 的流量倒入杯中,当水深为4cm时,则水面升高的瞬时变化率是
.
的流量倒入杯中,当水深为4cm时,则水面升高的瞬时变化率是
. 