题目内容
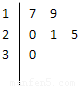
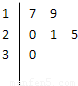
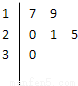
 某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.(1)根据茎叶图计算样本的平均值;
(2)日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,求恰有1名优秀工人的概率.
分析:(1)茎叶图中共同的数字是数字的十位,这是解决本题的突破口,根据所给的茎叶图数据,代入平均数公式求出结果;
(2)设“从该车间6名工人中,任取2人,恰有1名优秀工人”为事件A,结合组合数利用概率的计算公式即可求解事件A的概率.
(2)设“从该车间6名工人中,任取2人,恰有1名优秀工人”为事件A,结合组合数利用概率的计算公式即可求解事件A的概率.
解答:解:(1)平均数为
=22--(4分)
(2)解法一:将六名工人编号,ABCDEF,其中EF表示优秀工人,从6件产品中选2件,
其包含的基本事件为:(AB)(AC)(AD)(AE)(AF)(BC)(BD)(BE)(BF)(CD)(CE)(CF)(DE)(DF)(EF)共有15种,--(8分)
事件A表示2名工人中恰有1名优秀工人,事件A的基本事件为(AE)(AF)(BE)(BF)(CE)(CF)(DE)(DF)共8种,则P(A)=
--(13分)
答:2名工人中恰有1名优秀工人的概率为
.--(14分)
解法二:试验的所有结果共有
=15种,--(8分)
事件A表示2名工人中恰有1名优秀工人,事件A的结果共有
=8种,则P(A)=
--(13分)
答:2名工人中恰有1名优秀工人的概率为
.--(14分)
| 17+19+20+21+25+30 |
| 6 |
(2)解法一:将六名工人编号,ABCDEF,其中EF表示优秀工人,从6件产品中选2件,
其包含的基本事件为:(AB)(AC)(AD)(AE)(AF)(BC)(BD)(BE)(BF)(CD)(CE)(CF)(DE)(DF)(EF)共有15种,--(8分)
事件A表示2名工人中恰有1名优秀工人,事件A的基本事件为(AE)(AF)(BE)(BF)(CE)(CF)(DE)(DF)共8种,则P(A)=
| 8 |
| 15 |
答:2名工人中恰有1名优秀工人的概率为
| 8 |
| 15 |
解法二:试验的所有结果共有
| C | 2 6 |
事件A表示2名工人中恰有1名优秀工人,事件A的结果共有
| C | 1 2 |
| C | 1 4 |
| 8 |
| 15 |
答:2名工人中恰有1名优秀工人的概率为
| 8 |
| 15 |
点评:本题主要考查茎叶图的应用,古典概型及其概率计算公式,属于容易题.对于一组数据,通常要求的是这组数据的众数,中位数,平均数,题目分别表示一组数据的特征,考查最基本的知识点.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
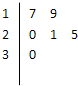 (2013•广东)某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
(2013•广东)某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.