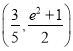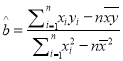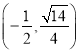题目内容
【题目】已知函数![]() 的图象与
的图象与![]() 轴正半轴交点的横坐标依次构成一个公差为
轴正半轴交点的横坐标依次构成一个公差为![]() 的等差数列,把函数
的等差数列,把函数![]() 的图象沿
的图象沿![]() 轴向右平移
轴向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,则下列叙述不正确的是( )
的图象,则下列叙述不正确的是( )
A. ![]() 的图象关于点
的图象关于点![]() 对称 B.
对称 B. ![]() 的图象关于直线
的图象关于直线![]() 对称
对称
C. ![]() 在
在![]() 上是增函数 D.
上是增函数 D. ![]() 是奇函数
是奇函数
【答案】C
【解析】f(x)= ![]() =2sin(ωx+
=2sin(ωx+![]() ),
),
由题意可知, ![]() ,则T=π,
,则T=π, ![]() ,
,
∴f(x)=2sin(ωx+![]() ),
),
∴g(x)=2sin[2(x﹣![]() )+
)+![]() ]=2sin2x.
]=2sin2x.
∵f(![]() )=2sin(﹣π)=0,∴g(x)的图象关于点(﹣
)=2sin(﹣π)=0,∴g(x)的图象关于点(﹣![]() ,0)对称,故A正确;
,0)对称,故A正确;
∵f(![]() )=2sin
)=2sin![]() =2,∴g(x)的图象关于直线x=
=2,∴g(x)的图象关于直线x=![]() 对称,故B正确;
对称,故B正确;
由x∈[![]() ,
, ![]() ],得2x∈[
],得2x∈[![]() ,π],可知g(x)在[
,π],可知g(x)在[![]() ,
, ![]() ]上是减函数,故C错误;
]上是减函数,故C错误;
由g(﹣x)=2sin(﹣x)=﹣2sin2x=﹣g(x),可得g(x)是奇函数,故D正确.
故选:C.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
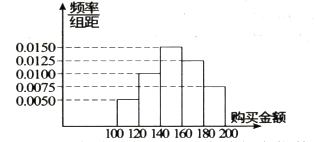
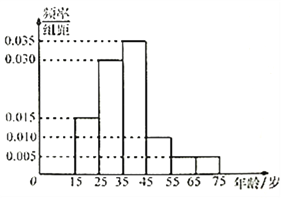
【题目】2017年5月14日,第一届“一带一路”国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在![]() 岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为:
岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为: ![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .把年龄落在区间
.把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年”和“中老年”.
内的人分别称为“青少年”和“中老年”.
(1)根据频率分布直方图求样本的中位数(保留两位小数)和众数
(2)根据已知条件完成下面的2×2列联表,并判断能否有99%的把握认为关注“带一路”是否和年龄段有关?
关注 | 不关注 | 合计 | |
青少年 | 15 | ||
中老年 | |||
合计 | 50 | 50 | 100 |
附:参考公式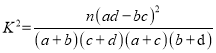 ,其中
,其中![]()
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |