题目内容
已知6sin2α+sinαcosα-2cos2α=0,cosα≠0,α∈(
解法一:由已知得(3sinα+2cosα)(2sinα-cosα)=0![]() 3sinα+2cosα=0或2sinα-cosα=0.
3sinα+2cosα=0或2sinα-cosα=0.
由已知条件可知cosα≠0,所以α≠![]() ,即α∈(
,即α∈(![]() ,π).
,π).
于是tanα<0.∴tanα=-![]() .
.
sin(2α+![]() )=sin2αcos
)=sin2αcos![]() +cos2αsin
+cos2αsin![]()
=sinαcosα+![]() (cos2α-sin2α)
(cos2α-sin2α)
=![]() +
+![]() ×
×![]()
=![]() +
+![]() ×
×![]() .
.
将tanα=-![]() 代入上式得
代入上式得
sin(2α+![]() )=
)=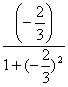 +
+![]() ×
×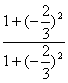 =-
=-![]() 即为所求.
即为所求.
解法二:由已知条件可知cosα≠0,则α≠![]() ,
,
所以原式可化为6tan2α+tanα-2=0,
即(3tanα+2)(2tanα-1)=0.
又∵α∈(![]() ,π),∴tanα<0.
,π),∴tanα<0.
∴tanα=-![]() .
.
下同解法一.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目