题目内容
已知函数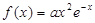 ,
,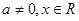 .
.
(I)讨论 的单调性.
的单调性.
(II)当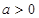 时,讨论关于
时,讨论关于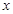 的方程
的方程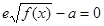 的实根的个数.
的实根的个数.
【答案】
(I)当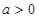 时,
时,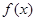 在
在 上单调递增,在
上单调递增,在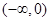 和
和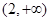 上单调递减. 当
上单调递减. 当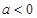 时,
时,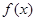 在
在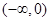 和
和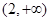 上单调递增,在
上单调递增,在 上单调递减(II)即
上单调递减(II)即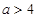 时,原方程有一解.
时,原方程有一解.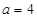 时,原方程有两解.
时,原方程有两解.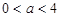 时,原方程有三解.
时,原方程有三解.
【解析】(I)依题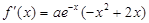 , ―――――――――――――――(1分)
, ―――――――――――――――(1分)
令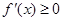 ,即:
,即: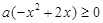 . ―――――――――――――――――――(2分)
. ―――――――――――――――――――(2分)
易知,当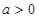 时,
时,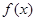 在
在 上单调递增, ―――――――――――――――(4分)
上单调递增, ―――――――――――――――(4分)
在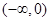 和
和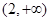 上单调递减. ――――――――――――――――――(6分)
上单调递减. ――――――――――――――――――(6分)
当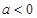 时,
时,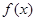 在
在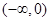 和
和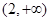 上单调递增, ――――――――――――(7分)
上单调递增, ――――――――――――(7分)
在 上单调递减. ―――――――――――――――――――――――――-(8分)
上单调递减. ―――――――――――――――――――――――――-(8分)
(II)由(I)知当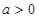 时,
时,
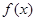 极小=
极小=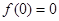 ,
,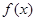 极大=
极大=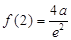 ――――――――――――――――(9分)
――――――――――――――――(9分)
又当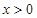 或
或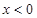 时,
时,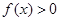 ,
,
可见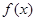 的图象如下: ――――――――――(10分)
的图象如下: ――――――――――(10分)
而方程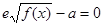 ,
,
转化为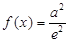 ――――――――――――(11分)
――――――――――――(11分)
可见,当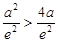 时,即
时,即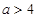 时,原方程有一解.
时,原方程有一解.
同理:
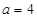 时,原方程有两解.
时,原方程有两解.
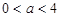 时,原方程有三解. ――――――――-(12分
时,原方程有三解. ――――――――-(12分
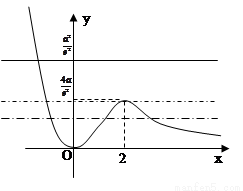

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, .
. ,
, 。
。 的单调区间;
的单调区间; ,曲线C与其在点
,曲线C与其在点 处的切线交于另一点
处的切线交于另一点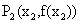 ,曲线C与其在点
,曲线C与其在点 ,线段
,线段
 (Ⅰ)(ii)的正确命题,并予以证明。
(Ⅰ)(ii)的正确命题,并予以证明。