题目内容
3.函数y=log32x的反函数是y=$\frac{1}{2}{•3}^{x}$,x∈R.分析 由y=log32x解得2x=3y,把x与y互换,即可得出.
解答 解:由y=log32x解得2x=3y,把x与y互换,可得:y=$\frac{1}{2}{•3}^{x}$.
∴函数y=log32x的反函数是y=$\frac{1}{2}{•3}^{x}$,x∈R.
故答案为:y=$\frac{1}{2}{•3}^{x}$,x∈R.
点评 本题考查了指数式与对数式互化、反函数的求法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
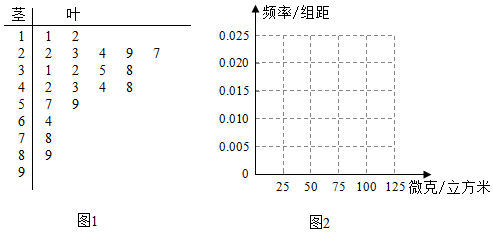
13.近期雾霾天气多发,对城市环境造成很大影响,某城市环保部门加强了对空气质量的监测.按国家环保部发布的(环境空气质量标准)规定,居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度的监测数据,数据记录如图1茎叶图
(1)完成如下的频率分布表,并在所给的坐标系(图2)中画出(0,100)的频率分布直方图;
(2)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
(1)完成如下的频率分布表,并在所给的坐标系(图2)中画出(0,100)的频率分布直方图;
(2)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
| 组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | ||
| 第二组 | (25,50] | ||
| 第三组 | (50,75] | ||
| 第四组 | (75,100] |

18.设△ABC中的内角A,B,C所对的边长分别为a,b,c,且asinB=2sin$\frac{A}{2}$,cos$\frac{A}{2}$=$\frac{2}{3}$,则b等于( )
| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{4}{3}$ |
15.已知函数f(x)=x2+4x,则f(2cosθ-1)的值域是( )
| A. | [-4,+∞) | B. | (-∞,-3] | C. | [-4,5] | D. | [-3,5] |
13.已知A、B、C为△ABC的三个内角,向量$\overrightarrow{m}$满足|$\overrightarrow{m}$|=$\frac{\sqrt{6}}{2}$,且$\overrightarrow{m}$=($\sqrt{2}$sin$\frac{B+C}{2}$,cos$\frac{B-C}{2}$),若A最大时,动点P使得|$\overrightarrow{PB}$|、|$\overrightarrow{BC}$|、|$\overrightarrow{PC}$|成等差数列,则$\frac{|\overrightarrow{PA}|}{|\overrightarrow{BC}|}$的最大值是( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{3\sqrt{2}}{4}$ |