题目内容
已知定点F(0，1)和直线l1：y=-l，过定点F与直线l1相切的动圆圆心为点C．
(Ⅰ)求动点C的轨迹方程；
(Ⅱ)过点F的直线l2交轨迹于两点P，Q，交直线l1于点R，求
的最小值。
(Ⅰ)求动点C的轨迹方程；
(Ⅱ)过点F的直线l2交轨迹于两点P，Q，交直线l1于点R，求
的最小值。 解：(Ⅰ)由题设点C到点F的距离等于它到l1的距离，点C的轨迹是以F为焦点，l1为准线的抛物线，
所求轨迹的方程为x2=4y。
(Ⅱ)由题意直线l2的方程为y=kx+l，与抛物线方程联立，消去y，得x2-4kx-4=0，
记P(x1，y1)，Q(x2，y2)，
则x1+x2=4k，x1x2=-4，
因为直线PQ的斜率k≠0，易得点R的坐标为
，
∵
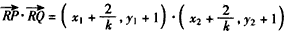
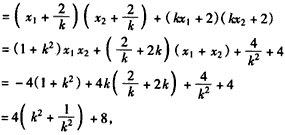
，当且仅当k2=1时取得等号，
∴
，即
的最小值为16。
所求轨迹的方程为x2=4y。
(Ⅱ)由题意直线l2的方程为y=kx+l，与抛物线方程联立，消去y，得x2-4kx-4=0，
记P(x1，y1)，Q(x2，y2)，
则x1+x2=4k，x1x2=-4，
因为直线PQ的斜率k≠0，易得点R的坐标为
， ∵
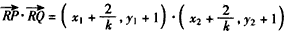
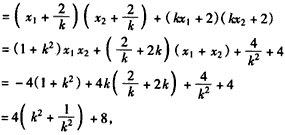
，当且仅当k2=1时取得等号，∴
，即的最小值为16。 
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
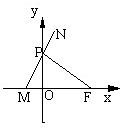如图，已知定点F（1，0），动点P在y轴上运动，过点P作PM⊥PF并交x轴于M点，延长MP到N，使|PN|=|PM|．
，动点P的轨迹为C，已知圆M过定点D(0，2)，圆心M在轨迹C上运动，且圆M与x轴交于A、B两点，设|DA|＝l1，|DB|＝l2，则
的最大值为
．
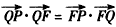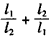的最大值．
，
的最大值。