题目内容
已知点F(0,1),直线l:y=-1,P为平面上的动点,过点P作直线l的垂线,垂足为Q,且![]() .
.
(1)求动点P的轨迹C的方程;
(2)已知圆M过定点D(0,2),圆心M在轨迹C上运动,且圆M与x轴交于A、B两点,设|DA|=l1,|DB|=l2,求![]() 的最大值.
的最大值.
答案:
解析:
提示:
解析:
|
(1)解:设 ∵ ∴ 即 所以动点 (2)解:设圆 圆 圆 令 整理得, 由①、②解得, 不妨设 ∴ ∴ 当 当且仅当 当 故当 |
提示:
|
本小题主要考查圆、抛物线、基本不等式等知识,考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力和运算求解能力 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
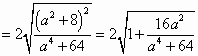 ,③
,③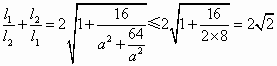 .
.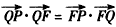 ,
,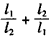 的最大值。
的最大值。