题目内容
7、n∈N+,Cn1+2Cn2+3Cn3+…+nCnn=
n2n-1
.分析:本题中所求和中的每一项kCnk刚好是二项式(1+x)n的通项Cnkxk的导数的系数,故可以先将二项式(1+x)n展开,然后两边求导,并将x取值为1即可求解为n2n-1.(此外本题也可以用倒序相加法求解)
解答:解:∵(1+x)n=Cn0+Cn1x1+Cn2x3+Cn3x3+…+Cnnxn,两边同时求导可得n(1+x)n-1=Cn1+2Cn2x1+3Cn3x2+…+nCnnxn-1
令x=1,得n2n-1=Cn1+2Cn2+3Cn3+…+nCnn,
故答案为n2n-1
令x=1,得n2n-1=Cn1+2Cn2+3Cn3+…+nCnn,
故答案为n2n-1
点评:本题主要考查二项式定理的应用,属于中等难度题型,在处理有关二项式定理有关系数问题时通常与二项式中x赋值有关.

练习册系列答案
相关题目
 )n<3.
)n<3.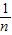 )n<3.
)n<3.