题目内容
设an=1+q+q2+…+qn-1(n∈N*,q≠±1),An=Cn1a1+Cn2a2+…+Cnnan.
(1)用q和n表示An;
(2)当-3<q<1时,求
.
(1)用q和n表示An;
(2)当-3<q<1时,求
| lim |
| n→∞ |
| An |
| 2n |
(1)因为q≠1,
所以an=1+q+q2+…+qn-1=
.
于是An=
Cn1+
Cn2+…+
Cnn
=
[(Cn1+Cn2+…+Cnn)-(Cn1q+Cn2q2+…+Cnnqn)]
=
{(2n-1)-[(1+q)n-1]}
=
[2n-(1+q)n].
(2)
=
[1-(
)n].
因为-3<q<1,且q≠-1,
所以0<|
|<1.
所以
=
.
所以an=1+q+q2+…+qn-1=
| 1-qn |
| 1-q |
于是An=
| 1-q |
| 1-q |
| 1-q2 |
| 1-q |
| 1-qn |
| 1-q |
=
| 1 |
| 1-q |
=
| 1 |
| 1-q |
=
| 1 |
| 1-q |
(2)
| An |
| 2n |
| 1 |
| 1-q |
| 1+q |
| 2 |
因为-3<q<1,且q≠-1,
所以0<|
| 1+q |
| 2 |
所以
| lim |
| n→∞ |
| An |
| 2n |
| 1 |
| 1-q |

练习册系列答案
相关题目
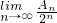 .
.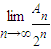 .
.