题目内容
已知定点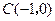 及椭圆
及椭圆 ,过点
,过点 的动直线与椭圆相交于
的动直线与椭圆相交于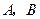 两点.
两点.
(Ⅰ)若线段 中点的横坐标是
中点的横坐标是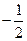 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)在 轴上是否存在点
轴上是否存在点 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
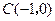 及椭圆
及椭圆 ,过点
,过点 的动直线与椭圆相交于
的动直线与椭圆相交于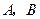 两点.
两点.(Ⅰ)若线段
 中点的横坐标是
中点的横坐标是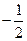 ,求直线
,求直线 的方程;
的方程;(Ⅱ)在
 轴上是否存在点
轴上是否存在点 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(Ⅰ) ,或
,或 (Ⅱ)
(Ⅱ) 
 ,或
,或 (Ⅱ)
(Ⅱ) 
(Ⅰ)解:依题意,直线 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为 ,
,
将 代入
代入 ,消去
,消去 整理得
整理得 ………….. 2分
………….. 2分
设 则
则 ………….. 4分
………….. 4分
由线段 中点的横坐标是
中点的横坐标是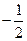 , 得
, 得 ,解得
,解得 ,适合
,适合 . ….. 5分
. ….. 5分
所以直线 的方程为
的方程为 ,或
,或 . ….. 6分
. ….. 6分
(Ⅱ)解:假设在 轴上存在点
轴上存在点 ,使
,使 为常数.
为常数.
①当直线 与
与 轴不垂直时,由(Ⅰ)知
轴不垂直时,由(Ⅰ)知 
所以
 ………….. 8分
………….. 8分
将 代入,整理得
代入,整理得

注意到 是与
是与 无关的常数,从而有
无关的常数,从而有 ,此时
,此时 .. 10分
.. 10分
②当直线 与
与 轴垂直时,此时点
轴垂直时,此时点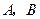 的坐标分别为
的坐标分别为 ,
,
当 时,亦有
时,亦有
综上,在 轴上存在定点
轴上存在定点 ,使
,使 为常数. ……………….. 12分
为常数. ……………….. 12分
 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为 ,
,将
 代入
代入 ,消去
,消去 整理得
整理得 ………….. 2分
………….. 2分设
 则
则 ………….. 4分
………….. 4分由线段
 中点的横坐标是
中点的横坐标是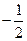 , 得
, 得 ,解得
,解得 ,适合
,适合 . ….. 5分
. ….. 5分所以直线
 的方程为
的方程为 ,或
,或 . ….. 6分
. ….. 6分(Ⅱ)解:假设在
 轴上存在点
轴上存在点 ,使
,使 为常数.
为常数.①当直线
 与
与 轴不垂直时,由(Ⅰ)知
轴不垂直时,由(Ⅰ)知 
所以

 ………….. 8分
………….. 8分将
 代入,整理得
代入,整理得

注意到
 是与
是与 无关的常数,从而有
无关的常数,从而有 ,此时
,此时 .. 10分
.. 10分②当直线
 与
与 轴垂直时,此时点
轴垂直时,此时点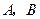 的坐标分别为
的坐标分别为 ,
,当
 时,亦有
时,亦有
综上,在
 轴上存在定点
轴上存在定点 ,使
,使 为常数. ……………….. 12分
为常数. ……………….. 12分
练习册系列答案
相关题目
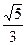 ,一条准线为y=3.
,一条准线为y=3. 的椭圆的一个焦点是(0,4),则此椭圆的准线方程为__________.
的椭圆的一个焦点是(0,4),则此椭圆的准线方程为__________.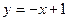 与椭圆
与椭圆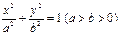 相交于A、B两点.。
相交于A、B两点.。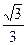 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;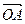 与向量
与向量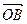 互相垂直(其中O为坐标原点),当椭圆的离心率e=2时,求椭圆的长轴的长.
互相垂直(其中O为坐标原点),当椭圆的离心率e=2时,求椭圆的长轴的长.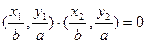 ,椭圆的离心率
,椭圆的离心率 短轴长为2,0为坐标原点.
短轴长为2,0为坐标原点.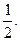 点
点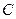 在
在 轴上,
轴上,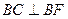 ,且
,且 、
、 三点确定的圆
三点确定的圆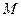 恰好与直线
恰好与直线 相切.
相切. 交椭圆于
交椭圆于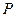 、
、 两点,在
两点,在 ,使得
,使得 恰好为△
恰好为△ 的内角平分线,若存在,求出点
的内角平分线,若存在,求出点
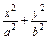 =1(a>b>0)上的三点,其中点
=1(a>b>0)上的三点,其中点 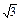 ,0),BC过椭圆的中心O,且AC⊥BC,|BC|=2|AC|.
,0),BC过椭圆的中心O,且AC⊥BC,|BC|=2|AC|.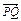 与
与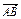 是否共线,并给出证明.
是否共线,并给出证明.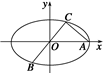
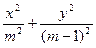 =1的准线平行于x轴,则m应满足的条件是( )
=1的准线平行于x轴,则m应满足的条件是( )