题目内容
已知椭圆 的中心在原点,一个焦点为
的中心在原点,一个焦点为 ,且长轴与短轴的比为
,且长轴与短轴的比为 .
.
(Ⅰ)求椭圆 的方程.
的方程.
(Ⅱ)若椭圆 在第一象限的一点P的横坐标为1,过点P作倾斜角互补的两条不同的直线PA,PB分别交椭圆C于另外两点A,B.求证:直线AB的斜率为定值.
在第一象限的一点P的横坐标为1,过点P作倾斜角互补的两条不同的直线PA,PB分别交椭圆C于另外两点A,B.求证:直线AB的斜率为定值.
解:(Ⅰ)由已知可设椭圆C的方程为:
依题意: 且
且 解得:
解得:
故椭圆C的方程为:
(Ⅱ)由(1)知:P (1, )
)
由已知知PA,PB的斜率必存在,设PA: 即:
即:
PB: 即:
即: ……6分
……6分
由 得:
得:
设 则:
则:
故: 同理:
同理:
直线AB的斜率

所以:直线AB的斜率为定值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的最小正周期是
的最小正周期是 ;
; 轴上的角的集合是
轴上的角的集合是 ;
; 的图象和函数
的图象和函数 的图象有三个公共点;
的图象有三个公共点; 的图象向右平移
的图象向右平移 个单位得到
个单位得到 的图象;
的图象; 在[
在[ ]上是减函数。
]上是减函数。 :
: ;
; :曲线
:曲线 与
与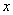 轴交于不同的两点.如果
轴交于不同的两点.如果 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围. 中,
中, 分别是角
分别是角 的对边,若
的对边,若 ,则
,则 等于
等于 B.
B.  C.
C.  D.
D. 
 符号
符号 表示不超过
表示不超过 的最大整数,若函数
的最大整数,若函数 有且仅有3个零点,则
有且仅有3个零点,则 的取值范围是
的取值范围是 B.
B. C.
C.  D.
D. 