题目内容
考察下列一组不等式:
|
分析:本题考查的知识点是归纳推理,我要根据已知的一组不等式:
,分析出不等号两边数据的变化规律,并进行归纳,进而归纳出一个一般性的式子.
|
解答:解:由不等式:
我们分析不等号两端式子结构的特点,及指数之间的关系
不难推断:
am+n+bm+n>ambn+anbm(a,b,m,n>0,且a≠b)
故选Am+n+bm+n>ambn+anbm(a,b,m,n>0,且a≠b)
|
我们分析不等号两端式子结构的特点,及指数之间的关系
不难推断:
am+n+bm+n>ambn+anbm(a,b,m,n>0,且a≠b)
故选Am+n+bm+n>ambn+anbm(a,b,m,n>0,且a≠b)
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

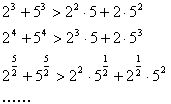 将上述不等式在左右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式为 ___。
将上述不等式在左右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式为 ___。