题目内容
已知A,B,C,是圆x2+y2=1上的三点,且
+
=
,其中O为坐标原点,
•
=
| OA |
| OB |
| OC |
| OA |
| OB |
-
| 1 |
| 2 |
-
.| 1 |
| 2 |
分析:由题意可得 |
| = |
| =1,∠AOC=∠COB=
,∠AOB=
,利用两个向量的数量积的定义可得
•
=|
| • |
| 的值.
| OA |
| OB |
| π |
| 3 |
| 2π |
| 3 |
| OA |
| OB |
| OA |
| OB |
解答:解:由题意可得 |
| = |
| =1,∠AOC=∠COB=
,∠AOB=
,
故
•
=|
| • |
|=1×1 cos
=-
,
故答案为-
.
| OA |
| OB |
| π |
| 3 |
| 2π |
| 3 |
故
| OA |
| OB |
| OA |
| OB |
| 2π |
| 3 |
| 1 |
| 2 |
故答案为-
| 1 |
| 2 |
点评:本题主要考查两个向量的数量积的定义,求出∠AOB=
,是解题的关键,属于基础题.
| 2π |
| 3 |

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
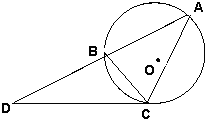 (1)圆O是△ABC的外接圆,过点C的圆的切线与AB的延长线交于点D,
(1)圆O是△ABC的外接圆,过点C的圆的切线与AB的延长线交于点D,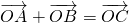 ,其中O为坐标原点,
,其中O为坐标原点, =________.
=________. ,AB=BC=3,求BD以及AC的长.
,AB=BC=3,求BD以及AC的长. ,曲线C1,C2相交于A,B两点
,曲线C1,C2相交于A,B两点
 ,其中O为坐标原点,
,其中O为坐标原点, = .
= .