Question

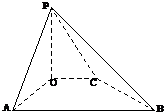（2008•卢湾区一模）（理）已知四边形OABC为直角梯形，∠AOC=∠OAB=90°，PO⊥平面AC，且OA=3，AB=6，OC=2，PO=3．若

PD

=

1

3

PB

，求：
（1）点D的坐标；
（2）异面直线PC与AD所成的角θ（用反三角函数值表示）．

Answer 1

分析：（1）建立空间直角坐标系，找到各定点的坐标，设出D点坐标，利用

PD

=

1

3

PB

即可求出D点坐标．
（2）利用空间向量，把所求异面直线所成角转化为空间向量的夹角，利用向量的夹角公式即可求出该角的余弦值，注意异面直线所成角的范围是（0，

π

2

]．再利用反余弦表示即可．

解答：解：（1）以OA所在直线为x轴，OC所在直线为y轴，OP所在直线为z轴，建立空间直角坐标系，
则P（0，0，3），B（3，6，0），A（3，0，0），C（0，2，0）
设D（x，y，z），则

PD

=（x，y，z-3），

PB

=（3，6，-3）
∵

PD

=

1

3

PB

，∴（x，y，z-3）=

1

3

（3，6，-3）
∴x=1，y=2，z=2
∴D（1，2，2）；
（2）∵

PC

=（0，2，-3），

AD

=（-2，2，2）
∴cos＜

PC

，

AD

＞=

PC • AD

| PC || AD |

=

4-6

4+9 4+4+4

=-

39

39

∴cosθ=

39

39

θ=arccos

39

39

．

点评：本题主要考查了利用空间向量解决立体几何中异面直线所成角的大小．