题目内容
已知等比数列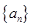 的各项均为正数,且
的各项均为正数,且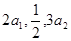 成等差数列,
成等差数列,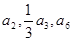 成等比数列.
成等比数列.
(1)求数列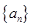 的通项公式;
的通项公式;
(2)已知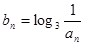 ,记
,记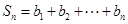 ,
,
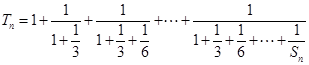 ,求证:
,求证: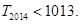
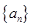 的各项均为正数,且
的各项均为正数,且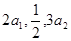 成等差数列,
成等差数列,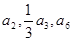 成等比数列.
成等比数列.(1)求数列
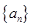 的通项公式;
的通项公式;(2)已知
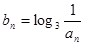 ,记
,记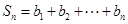 ,
,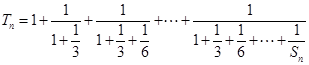 ,求证:
,求证: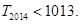
(1)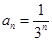 ;(2)参考解析
;(2)参考解析
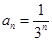 ;(2)参考解析
;(2)参考解析试题分析:(1)又等比数列
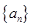 的各项均为正数,且
的各项均为正数,且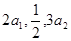 成等差数列,
成等差数列,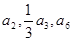 成等比数列.
成等比数列.可得到两个等式,解方程组可得结论.
(2)由(1)可得数列
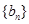 的通项,即可计算
的通项,即可计算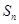 ,由于
,由于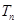 是一个复合的形式,所以先计算通项式
是一个复合的形式,所以先计算通项式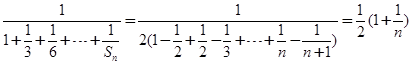 .即可得到
.即可得到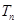 .又由于
.又由于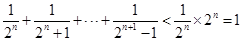 .即可得到结论.
.即可得到结论.试题解析:设等比数列
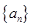 的公比为
的公比为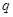 ,依题意可得
,依题意可得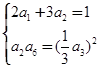 解得
解得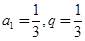 .所以通项
.所以通项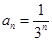 .
.(2)由(1)得
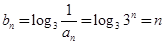 .所以
.所以 .由
.由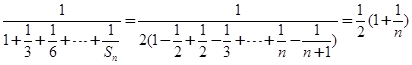 .所以
.所以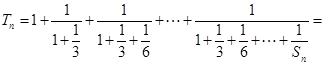
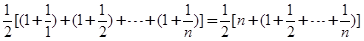 .所以
.所以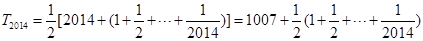 即等价于证明
即等价于证明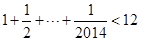 .
. .所以
.所以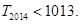

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
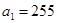 ,
,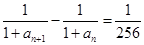
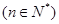 ,
,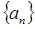 的通项公式
的通项公式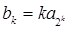 (
(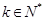 ),记数列
),记数列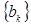 的前k项和为
的前k项和为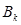 ,求
,求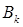 的最大值.
的最大值.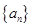 中,
中,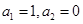 其前
其前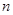 项和
项和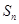 满足:
满足:

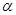 为锐角,且
为锐角,且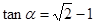 ,函数
,函数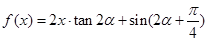 ,数列
,数列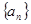 的首项
的首项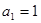 ,
,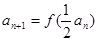 .
. 的表达式;(2)求数列
的表达式;(2)求数列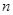 项和
项和 .
.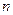 项和,若a1,a2,a5成等比数列,则S8="(" )
项和,若a1,a2,a5成等比数列,则S8="(" ) ,在验证n=1成立时,等式左边是
,在验证n=1成立时,等式左边是 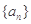 中,
中,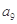 =
=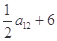 ,则数列
,则数列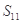 =( ).
=( ).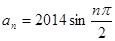 ,则
,则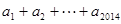 =( )
=( ) 的前n项和为
的前n项和为 ,若
,若 ,则必定有
,则必定有


