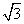题目内容
已知曲线 . (1)求曲线在
. (1)求曲线在 处的切线方程;(2)求曲线过点
处的切线方程;(2)求曲线过点 的切线方程.
的切线方程.
解(1)∵y′=x2,则在点P(2,4)处的切线的斜率k=y′|x=2=4----------------(2分)
∴曲线在点P(2,4)处的切线方程为y-4=4(x-2),即4x-y-4=0 -----------------(4分)
(2)设曲线y= x3+
x3+ 与过点P(2,4)的切线相切于点A(x0,
与过点P(2,4)的切线相切于点A(x0, x03+
x03+ ),则切线的斜率
),则切线的斜率
k=y′| =x02
=x02
∴切线方程为y-( x03+
x03+ )=x02(x-x0),即y=x02·x-
)=x02(x-x0),即y=x02·x- x03+
x03+ --------------------(6分)
--------------------(6分)
∵点P(2,4)在切线上,∴4=2x02- x03+
x03+ ,
,
即x03-3x02+4=0,整理可得x03+x02-4x02+4=0, 解得x0=-1或x0=2-----------------(8分)
故所求的切线方程为4x-y-4=0或x-y+2=0. --------------------------------(10分)

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
某学生对一些对数进行运算,如下图表格所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
现在发觉学生计算中恰好有两次地方出错,那么出错的数据是 ( )
A.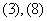 B.
B.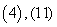 C.
C.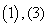 D.
D.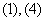
 的两个焦点,点P在双曲线上,且
的两个焦点,点P在双曲线上,且 则
则 的值为 ( )
的值为 ( ) C.4 D.8
C.4 D.8





 (1)
(1) (2)
(2) (3)
(3) (4)
(4)



 (5)
(5) (6)
(6) (7)
(7) (8)
(8)


 (9)
(9) (10)
(10) (11)
(11) 在正方形
在正方形 所在平面外,
所在平面外, ,
, 与
与 所成角的大小为( )
所成角的大小为( ) B.
B. C.
C. D.
D.
 且
且 ,则使不等式
,则使不等式 恒成立的实数
恒成立的实数 的取值范围__________________.
的取值范围__________________. ,
,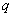 .若
.若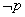 是
是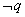 的 ( )
的 ( ) 充要条件
充要条件  (D ) 既不充分也不必要条
(D ) 既不充分也不必要条 件
件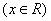 满足f(
满足f(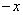 )=f(x),f(x)=f(2
)=f(x),f(x)=f(2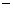 x),且当
x),且当 时,f(x)=x3.又函数g(x)=|xcos
时,f(x)=x3.又函数g(x)=|xcos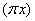 |,则函数h(x)=g(x)-f(x)在
|,则函数h(x)=g(x)-f(x)在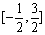 上的零点个数为
上的零点个数为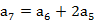 ,若存在两项
,若存在两项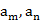 ,使得
,使得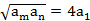 ,则
,则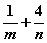 的最小值为( )
的最小值为( ) B.
B. C.
C. D.不存在
D.不存在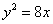 的焦点与双曲线
的焦点与双曲线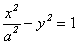 的一个焦点重合,则该双曲线
的一个焦点重合,则该双曲线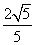 B.
B.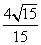 C.
C.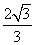 D.
D.