题目内容
如图，△ABC中，∠C=90°，且AC＝BC＝4，点M满足
，则
＝( )
| A．2 | B．3 | C．4 | D．6 |
C
解析试题分析：由于△ABC中，∠C =90°，且AC＝BC＝4，点M满足，又因为
,
.所以
.所以
.故选C.
考点：1.向量的加减法运算.2.向量的数量积.
练习册系列答案
全能练考卷系列答案
相关题目
已知向量
，
，若
与
垂直，则实数
A． | B． | C． | D． |
已知非零向量
与
满足(
+
)·
=0且·=
, 则△ABC为( )
| A．等腰直角三角形 | B．直角三角形 | C．等腰非等边三角形 | D．等边三角形 |
已知圆O的半径为1，PA，PB为该圆的两条切线，A，B为两切点，那么
的最小值等于.( )
A． | B． | C． | D． |
如图所示，
是圆
上的三个点，
的延长线与线段
交于圆内一点
,若
，则（ ）
A． | B． | C． | D． |
已知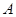
、
、
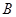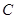是单位圆上三个互不相同的点.若
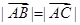，则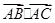
的最小值是（ ）
A． ． | B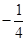． ． | C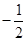． ． | D． ． |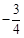
已知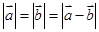
，则
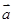与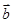
的夹角为（ ）
A． | B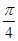． | C． | D． |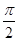
设P是曲线y=
上一点,点P关于直线y=x的对称点为Q,点O为坐标原点,则
·
=( )
| A．0 | B．1 | C．2 | D．3 |
设E,F分别是Rt△ABC的斜边BC上的两个三等分点,已知AB=3,AC=6,则
·
的值为( )
| A．6 | B．8 | C．10 | D．4 |