题目内容
在直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=AD=
CD=1,M是AB的中点,且
=2
,则
•
的值为( )
| 1 |
| 2 |
| BN |
| ND |
| CM |
| AN |

A、
| ||
B、-
| ||
C、
| ||
D、-
|
分析:根据平面向量加法的三角形法则,我们易将向量
,
进行分解,根据,AB∥CD,∠BAD=90°,且AB=AD=
CD=1,我们易得到
•
的值.
| CM |
| AN |
| 1 |
| 2 |
| CM |
| AN |
解答:解:∵AB=AD=
CD=1
又∵AB∥CD,∠BAD=90°,
∴
2=
2=1,
•
=0
=
+
+
=-
-
又∵
=2
∴
=
+
∴
•
=(-
-
)•(
+
)
=-
2-
2-
•
=-
-
=-
故选:D
| 1 |
| 2 |
又∵AB∥CD,∠BAD=90°,
∴
| AD |
| AB |
| AB |
| AD |
| CM |
| CD |
| DA |
| AM |
| AD |
| 3 |
| 2 |
| AB |
又∵
| BN |
| ND |
∴
| AN |
| 2 |
| 3 |
| AD |
| 1 |
| 3 |
| AB |
∴
| CM |
| AN |
| AD |
| 3 |
| 2 |
| AB |
| 2 |
| 3 |
| AD |
| 1 |
| 3 |
| AB |
=-
| 2 |
| 3 |
| AD |
| 1 |
| 2 |
| AB |
| 4 |
| 3 |
| AB |
| AD |
=-
| 2 |
| 3 |
| 1 |
| 2 |
=-
| 7 |
| 6 |
故选:D
点评:本题考查的知识点是平面向量数量积的运算,其中将向量
,
分解为
和
的形式,是解答本题的关键.
| CM |
| AN |
| AB |
| AD |

练习册系列答案
相关题目
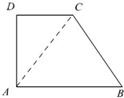
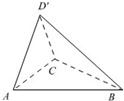
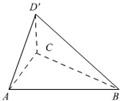
 (2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
(2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
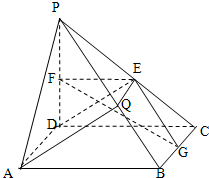
 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD= 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为