若ai＞0,且a1+a2+-+an=1,求证:a12+a22+-+an2≥(n∈N且n≥2). 题目和参考答案——青夏教育精英家教网——

题目内容

若a_i＞0(i=1,2,…,n),且a₁+a₂+…+a_n=1,

求证：a₁²+a₂²+…+a_n²≥(n∈N且n≥2).

证明：(1)n=2时，∵a₁+a₂=1,∴a₁²+a₂²=a₁²+(1-a₁)²=2(a₁-)²+≥.

∴n=2时命题正确.

（2）假设n=k(k≥2)时命题正确，即如果a₁+a₂+…+a_k=1且a_i＞0(i=1,2,…,k),

那么a₁²+a₂²+…+a_k²≥,则n=k+1时，

∵a₁+a₂+…+a_k+a_k+1=1,

∴a₁+a₂+…+a_k=1-a_k+1.

∵0＜a_k+1＜1,∴0＜1-a_k+1＜1.

∴k个正数的和=1,从而由归纳假设得

,

即a₁²+a₂²+…+a_k²≥(1-a_k+1)²,从而有a₁²+a₂²+…+a_k²+a_k+1²≥(1-a_k+1)²+a_k+1².

下面只要证明(1-a_k+1)²+a_k+1²≥,

即证(k+1)²a_k+1²-2(k+1)a_k+1+1≥0，

即证［(k+1)a_k+1-1］²≥0,∴上式成立.

故n=k+1时命题正确.

练习册系列答案

本土教辅名校学案初中生辅导系列答案

轻巧夺冠青岛专用系列答案

名题文化步步高书系名题系列答案

倍速训练法一练通系列答案

金牌教辅夺冠金卷系列答案

海淀名师名校百分卷系列答案

8848高中同步学情跟进卷系列答案

中考实战名校在招手系列答案

培优三好生系列答案

伴你学山西系列答案

相关题目

（2012•西城区一模）对于数列A：a₁，a₂，a₃（a_i∈N，i=1，2，3），定义“T变换”：T将数列A变换成数列B：b₁，b₂，b₃，其中b_i=|a_i-a_i+1|（i=1，2），且b₃=|a₃-a₁|．这种“T变换”记作B=T（A）．继续对数列B进行“T变换”，得到数列C：c₁，c₂，c₃，依此类推，当得到的数列各项均为0时变换结束．
（Ⅰ）试问A：2，6，4经过不断的“T变换”能否结束？若能，请依次写出经过“T变换”得到的各数列；若不能，说明理由；
（Ⅱ）设A：a₁，a₂，a₃，B=T（A）．若B：b，2，a（a≥b），且B的各项之和为2012．
（ⅰ）求a，b；
（ⅱ）若数列B再经过k次“T变换”得到的数列各项之和最小，求k的最小值，并说明理由．

（2012•泉州模拟）计算机内部都以二进制字符表示信息．若u=（a₁，a₂，…，a_n），其中a_i=0或1（i=1，2，…，n），则称u是长度为n的字节；设u=（a₁，a₂，…，a_n），v=（b₁，b₂，…，b_n），用d（u，v）表示满足a_i≠b_i（i=1，2，…，n）的i的个数．如u=（0，0，0，1），v=（1，0，0，1），则d（u，v）=1．现给出以下三个命题：
①若u=（a₁，a₂，…，a_n），v=（b₁，b₂，…，b_n），则0≤d（u，v）≤n；
②对于给定的长度为n的字节u，满足d（u，v）=n-1的长度为n的字节v共有n-1个；
③对于任意的长度都为n的字节u，v，w，恒有d（u，v）≤d（w，u）+d（w，v）．
则其中真命题的序号是（　　）

如图，P₁(x₁，y₁)，P₂(x₂，y₂)，…，P_n(x_n，y_n)(0＜y₁＜y₂＜…＜y_n，n∈N*)是曲线C：y²=3x(y≥0)上的n个点，点A_i(a_i，0)(i=1，2，3，…，n)在x轴的正半轴上，△A_i-1A_iP_i是正三角形(A₀是坐标原点)，
(1)求a₁，a₂，a₃；
(2)求出点A_n(a_n，0)(n∈N*)的横坐标a_n关于n的表达式；
(3)设

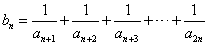，若对任意正整数n，当m∈[-1，1]时，不等式t²-mt+

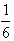＞b_n恒成立，求实数t的取值范围。

若a_i＞0(i=1,2,…,n),且a₁+a₂+…+a_n=1,

求证：a₁²+a₂²+…+a_n²≥(n∈N且n≥2).