题目内容
如图,在正三棱锥 中,
中, 分别是
分别是 的中点,
的中点, ,且
,且 ,则正三棱锥
,则正三棱锥 的体积是( )
的体积是( )
A. | B. | C. | D. |
B
解析试题分析:如图,取线段 的中点
的中点 ,连接
,连接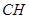 ,则依题意可知
,则依题意可知 ,且顶点
,且顶点 在底面
在底面 的射影
的射影 落在
落在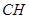 上,所以由
上,所以由 面
面 可得
可得 ,而
,而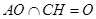 ,所以由线面垂直的判定定理可得
,所以由线面垂直的判定定理可得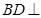 平面
平面 ,所以有
,所以有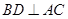 ,而
,而 是边
是边 的中点,所以
的中点,所以 ,而
,而 ,所以
,所以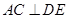 ,而
,而 ,由线面垂直的判定定理又可以得到
,由线面垂直的判定定理又可以得到 平面
平面 ,再结合三棱锥
,再结合三棱锥 为正三棱锥且
为正三棱锥且 ,所以该正三棱锥的侧棱两两垂直且
,所以该正三棱锥的侧棱两两垂直且 ,所以
,所以 ,故选B.
,故选B.
考点:1.空间中的垂直问题;2.三棱锥的体积问题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
某三棱锥的三视图如图所示,则该三棱锥的体积是( ).
A. | B. |
C. | D. |
一个几何体的三视图如图所示,则该几何体的体积为( )
A. | B. | C. | D. |
某几何体的三视图如图所示,则该几何体的体积为( )
A. | B. | C. | D. |
某三棱锥的三视图如图所示,该三棱锥的体积为( )
A. | B. | C. | D. |
某三棱椎的三视图如图所示,该三棱锥的四个面的面积中,最大的是( )
A. | B. | C. | D.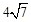 |
已知一个几何体的三视图如下图,则该几何体的体积为( ).
A.8- | B.8- |
C.4- | D.4- |
 的底面是正三角形,各条侧棱均相等,
的底面是正三角形,各条侧棱均相等,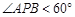 . 设点
. 设点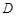 、
、 分别在线段
分别在线段 、
、 上,且
上,且 ,记
,记 ,
, 周长为
周长为 ,则
,则 的图象可能是( )
的图象可能是( )
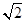 的正方形
的正方形 沿对角线
沿对角线 折起,连结
折起,连结 ,得到三棱锥
,得到三棱锥 ,其正视图、俯视图均为全等的等腰直角三角形(如图所示),则其侧视图的面积为( )
,其正视图、俯视图均为全等的等腰直角三角形(如图所示),则其侧视图的面积为( )