题目内容
如下图所示,菱形ABCD的边长为1,锐角A=60°,作它的内接△AEF,使E、F分别在BC和CD上,并且CD⊥EF,则△AEF面积的最大值为________________.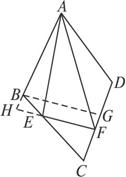
思路解析:要确定以△AEF面积S为因变量的解析式,关键是对与面积有关的自变量的选择.要搞清自变量与动△AEF的变化规律,要以能使运算简捷为原则选择自变量.
如图所示,过点B作BG⊥CD于点G,则CG=![]() ,AB的延长线与FE的延长线交于点H,
,AB的延长线与FE的延长线交于点H,
∵CD⊥EF,
∴AH⊥EF,BH=FG.
∴AH为△AEF的高,AH=AB+BH=AB+FG.
设CE=x,则EF=![]() ,CF=
,CF=![]() ,FG=CG-FG=
,FG=CG-FG=![]() -
-![]() =
=![]() ,
,
∴AH=1+![]() =
=![]() .
.
∴S△AEF=![]() ×EF×AH=
×EF×AH=![]() ×
×![]() ×
×![]() =
=![]() (-
(-![]() x2+3
x2+3![]() x).
x).
∵x∈(0,1],S在(0,1]上是增函数,
∴当x=1时,△AEF有最大值![]() .
.

答案:![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
