题目内容
若F1,F2是椭圆
思路解析:设G(x,y),P(5cosθ,4sinθ),而F1(-3,0),F2(3,0).
由重心坐标公式,得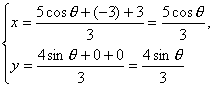 (θ为参数).
(θ为参数).
消参,得点G的轨迹方程为![]() =1.
=1.
答案:![]() =1
=1

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
题目内容
若F1,F2是椭圆
思路解析:设G(x,y),P(5cosθ,4sinθ),而F1(-3,0),F2(3,0).
由重心坐标公式,得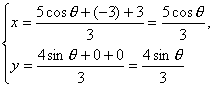 (θ为参数).
(θ为参数).
消参,得点G的轨迹方程为![]() =1.
=1.
答案:![]() =1
=1

 金博士一点全通系列答案
金博士一点全通系列答案