ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥÷–―ßΡβ‘ΎΗΏ“Μœ¬―ßΤΎΩΣ…η”Έ”Ψ―Γ–όΩΈΘ§ΈΣΝΥΝΥΫβΗΏ“Μ―ß…ζœ≤ΜΕ”Έ”Ψ «Ζώ”κ–‘±π”–ΙΊΘ§œ÷¥”ΗΏ“Μ―ß…ζ÷–≥ι»Γ![]() »ΥΉωΒς≤ιΘ§ΒΟΒΫ»γœ¬
»ΥΉωΒς≤ιΘ§ΒΟΒΫ»γœ¬![]() Ν–ΝΣ±μΘΚ
Ν–ΝΣ±μΘΚ

“―÷Σ‘Ύ’β![]() »Υ÷–ΥφΜζ≥ι»Γ“Μ»Υ≥ιΒΫœ≤ΜΕ”Έ”ΨΒΡ―ß…ζΒΡΗ≈¬ ΈΣ
»Υ÷–ΥφΜζ≥ι»Γ“Μ»Υ≥ιΒΫœ≤ΜΕ”Έ”ΨΒΡ―ß…ζΒΡΗ≈¬ ΈΣ![]() Θ§
Θ§
Θ®ΔώΘ©«κΫΪ…œ ωΝ–ΝΣ±μ≤Ι≥δΆξ’ϊΘ§≤Δ≈–Εœ «Ζώ”–![]() ΘΞΒΡΑ―Έ’»œΈΣœ≤ΜΕ”Έ”Ψ”κ–‘±π”–ΙΊΘΩ≤ΔΥΒΟςΡψΒΡάμ”…ΘΜ
ΘΞΒΡΑ―Έ’»œΈΣœ≤ΜΕ”Έ”Ψ”κ–‘±π”–ΙΊΘΩ≤ΔΥΒΟςΡψΒΡάμ”…ΘΜ
Θ®ΔρΘ©’κΕ‘Έ ΨμΒς≤ιΒΡ![]() Οϊ―ß…ζΘ§―ß–ΘΨωΕ®¥”œ≤ΜΕ”Έ”ΨΒΡ»Υ÷–Α¥Ζ÷≤ψ≥ι―υΒΡΖΫΖ®ΥφΜζ≥ι»Γ
Οϊ―ß…ζΘ§―ß–ΘΨωΕ®¥”œ≤ΜΕ”Έ”ΨΒΡ»Υ÷–Α¥Ζ÷≤ψ≥ι―υΒΡΖΫΖ®ΥφΜζ≥ι»Γ![]() »Υ≥…ΝΔ”Έ”ΨΩΤΤ’÷Σ Ε–ϊ¥ΪΉιΘ§≤Δ‘Ύ’β
»Υ≥…ΝΔ”Έ”ΨΩΤΤ’÷Σ Ε–ϊ¥ΪΉιΘ§≤Δ‘Ύ’β![]() »Υ÷–»Έ―ΓΝΫ»ΥΉςΈΣ–ϊ¥ΪΉιΒΡΉι≥ΛΘ§«σ’βΝΫ»Υ÷–÷Ν…Ό”–“ΜΟϊ≈°…ζΒΡΗ≈¬ Θ§≤ΈΩΦΙΪ ΫΘΚ
»Υ÷–»Έ―ΓΝΫ»ΥΉςΈΣ–ϊ¥ΪΉιΒΡΉι≥ΛΘ§«σ’βΝΫ»Υ÷–÷Ν…Ό”–“ΜΟϊ≈°…ζΒΡΗ≈¬ Θ§≤ΈΩΦΙΪ ΫΘΚ  ,Τδ÷–
,Τδ÷–![]() .≤ΈΩΦ ΐΨίΘΚ
.≤ΈΩΦ ΐΨίΘΚ

ΓΨ¥πΑΗΓΩΘ®ΔώΘ©”–![]() ΘΞΒΡΑ―Έ’»œΈΣœ≤ΜΕ”Έ”Ψ”κ–‘±π”–ΙΊΘΜΘ®ΔρΘ©
ΘΞΒΡΑ―Έ’»œΈΣœ≤ΜΕ”Έ”Ψ”κ–‘±π”–ΙΊΘΜΘ®ΔρΘ© ![]() .
.
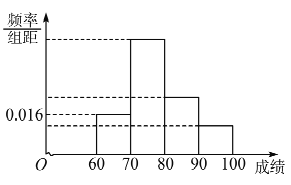
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®ΔώΘ©ΗυΨί‘Ύ100»Υ÷–ΥφΜζ≥ι»Γ1»Υ≥ιΒΫœ≤ΜΕ”Έ”ΨΒΡ―ß…ζΒΡΗ≈¬ ΈΣ![]() Θ§Ω…ΒΟœ≤Α°”Έ”ΨΒΡ―ß…ζΘ§Φ¥Ω…ΒΟΒΫΝ–ΝΣ±μΘΜάϊ”ΟΙΪ Ϋ«σΒΟ
Θ§Ω…ΒΟœ≤Α°”Έ”ΨΒΡ―ß…ζΘ§Φ¥Ω…ΒΟΒΫΝ–ΝΣ±μΘΜάϊ”ΟΙΪ Ϋ«σΒΟ![]() Θ§”κΝΌΫγ÷Β±»ΫœΘ§Φ¥Ω…ΒΟΒΫΫα¬έΘΜΘ®ΔρΘ©άϊ”ΟΝ–ΨΌΖ®Θ§»ΖΕ®Μυ±Ψ ¬ΦΰΒΡΗω ΐΈΣ15Θ§
Θ§”κΝΌΫγ÷Β±»ΫœΘ§Φ¥Ω…ΒΟΒΫΫα¬έΘΜΘ®ΔρΘ©άϊ”ΟΝ–ΨΌΖ®Θ§»ΖΕ®Μυ±Ψ ¬ΦΰΒΡΗω ΐΈΣ15Θ§ ![]() ΑϋΚ§
ΑϋΚ§![]() ÷÷«ιΩωΘ§Φ¥Ω…«σ≥ωΗ≈¬ .
÷÷«ιΩωΘ§Φ¥Ω…«σ≥ωΗ≈¬ .
‘ΧβΫβΈωΘΚΘ®ΔώΘ©”…“―÷ΣΩ…ΒΟΘΚœ≤ΜΕ”Έ”ΨΒΡ»ΥΙ≤![]() Θ§≤Μœ≤ΜΕ”Έ”ΨΒΡ”–ΘΚ
Θ§≤Μœ≤ΜΕ”Έ”ΨΒΡ”–ΘΚ ![]() »ΥΘ§
»ΥΘ§
”÷”…±μΩ…÷Σœ≤ΜΕ”Έ”ΨΒΡ»Υ≈°…ζ![]() »ΥΘ§Υυ“‘œ≤ΜΕ”Έ”ΨΒΡΡ–…ζ”–
»ΥΘ§Υυ“‘œ≤ΜΕ”Έ”ΨΒΡΡ–…ζ”–![]() »ΥΘ§
»ΥΘ§
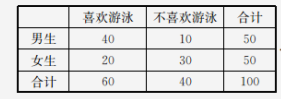
≤Μœ≤ΜΕ”Έ”ΨΒΡΡ–…ζ”–»ΥΘ§Υυ“‘≤Μœ≤ΜΕ”Έ”ΨΒΡ≈°…ζ”–40-10=30»Υ
”…¥ΥΘΚΆξ’ϊΒΡΝ–±μ»γœ¬ΘΚ
“ρΈΣ![]()
Υυ“‘”–![]() ΘΞΒΡΑ―Έ’»œΈΣœ≤ΜΕ”Έ”Ψ”κ–‘±π”–ΙΊ.
ΘΞΒΡΑ―Έ’»œΈΣœ≤ΜΕ”Έ”Ψ”κ–‘±π”–ΙΊ.
Θ®ΔρΘ©¥”œ≤ΜΕ”Έ”ΨΒΡ![]() »Υ÷–Α¥Ζ÷≤ψ≥ι―υΒΡΖΫΖ®ΥφΜζ≥ι»Γ
»Υ÷–Α¥Ζ÷≤ψ≥ι―υΒΡΖΫΖ®ΥφΜζ≥ι»Γ![]() »Υ≥…ΝΔ”Έ”ΨΩΤΤ’÷Σ Ε–ϊ¥ΪΉιΘ§Τδ÷–Ρ–…ζ”Π≥ι»Γ
»Υ≥…ΝΔ”Έ”ΨΩΤΤ’÷Σ Ε–ϊ¥ΪΉιΘ§Τδ÷–Ρ–…ζ”Π≥ι»Γ![]() »ΥΘ§Ζ÷±π…ηΈΣ
»ΥΘ§Ζ÷±π…ηΈΣ![]() ΘΜ≈°…ζ”Π≥ι»Γ
ΘΜ≈°…ζ”Π≥ι»Γ![]() »ΥΘ§Ζ÷±π…ηΈΣ
»ΥΘ§Ζ÷±π…ηΈΣ![]() Θ§œ÷¥”’β
Θ§œ÷¥”’β![]() »Υ÷–»Έ»Γ
»Υ÷–»Έ»Γ![]() »ΥΉςΈΣ–ϊ¥ΪΉιΒΡΉι≥ΛΘ§Ι≤”–
»ΥΉςΈΣ–ϊ¥ΪΉιΒΡΉι≥ΛΘ§Ι≤”–![]() ÷÷«ιΩωΘ§Ζ÷±πΈΣΘΚ
÷÷«ιΩωΘ§Ζ÷±πΈΣΘΚ ![]()
»τΦ«![]() ΓΑΝΫ»Υ÷–÷Ν…Ό”–“ΜΟϊ≈°…ζΒΡΗ≈¬ Γ±Θ§‘ρ
ΓΑΝΫ»Υ÷–÷Ν…Ό”–“ΜΟϊ≈°…ζΒΡΗ≈¬ Γ±Θ§‘ρ![]() ΑϋΚ§
ΑϋΚ§![]() ÷÷«ιΩωΘ§Ζ÷±πΈΣΘΚ
÷÷«ιΩωΘ§Ζ÷±πΈΣΘΚ ![]() ,Υυ“‘
,Υυ“‘![]()

 –Γ―ßΫΧ≤Ρ»Ϊ≤βœΒΝ–¥πΑΗ
–Γ―ßΫΧ≤Ρ»Ϊ≤βœΒΝ–¥πΑΗ –Γ―ß ΐ―ßΩΎΥψΧβΩ®Ά―ΩΎΕχ≥ωœΒΝ–¥πΑΗ
–Γ―ß ΐ―ßΩΎΥψΧβΩ®Ά―ΩΎΕχ≥ωœΒΝ–¥πΑΗ ”≈–ψ…ζ”Π”ΟΧβΩ®ΩΎΥψΧλΧλΝΖœΒΝ–¥πΑΗ
”≈–ψ…ζ”Π”ΟΧβΩ®ΩΎΥψΧλΧλΝΖœΒΝ–¥πΑΗ ’ψΫ≠÷°–«ΩΈ ±”≈Μ·Ής“ΒœΒΝ–¥πΑΗ
’ψΫ≠÷°–«ΩΈ ±”≈Μ·Ής“ΒœΒΝ–¥πΑΗ