题目内容
在数列{an}中,已知 ,若不等式3m-2≥an对任何3m-2≥an对任何n∈N*恒成立,则实数m的取值范围是
,若不等式3m-2≥an对任何3m-2≥an对任何n∈N*恒成立,则实数m的取值范围是
- A.[1,+∞)
- B.(0,+∞)
- C.(-∞,1]
- D.(1,+∞)
A
分析:由 ,猜想:
,猜想: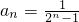 .再用数学归纳法证明
.再用数学归纳法证明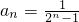 .故3m-2≥an=
.故3m-2≥an= 对任何n∈N*恒成立,等价于
对任何n∈N*恒成立,等价于 ≥3对任何n∈N*恒成立,由此能求出实数m的取值范围.
≥3对任何n∈N*恒成立,由此能求出实数m的取值范围.
解答:∵知 ,
,
∴ =
= ,
,
 ,
,
 ,
,
猜想: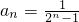 .
.
用数学归纳法证明:
①当n=1时, 成立;
成立;
②假设n=k时,成立,即 ,
,
则n=k+1时, =
= =
= =
= ,也成立,
,也成立,
故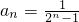 .
.
∵3m-2≥an= 对任何n∈N*恒成立,
对任何n∈N*恒成立,
∴ ≥3对任何n∈N*恒成立,
≥3对任何n∈N*恒成立,
∴m≥1,
故选A.
点评:本题考查数列与不等式的综合运用,解题时要认真审题,合理猜想,并用数学归纳法证明猜想.注意等价转化思想的合理运用.
分析:由
 ,猜想:
,猜想: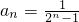 .再用数学归纳法证明
.再用数学归纳法证明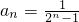 .故3m-2≥an=
.故3m-2≥an= 对任何n∈N*恒成立,等价于
对任何n∈N*恒成立,等价于 ≥3对任何n∈N*恒成立,由此能求出实数m的取值范围.
≥3对任何n∈N*恒成立,由此能求出实数m的取值范围.解答:∵知
 ,
,∴
 =
= ,
, ,
, ,
,猜想:
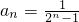 .
.用数学归纳法证明:
①当n=1时,
 成立;
成立;②假设n=k时,成立,即
 ,
,则n=k+1时,
 =
= =
= =
= ,也成立,
,也成立,故
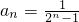 .
.∵3m-2≥an=
 对任何n∈N*恒成立,
对任何n∈N*恒成立,∴
 ≥3对任何n∈N*恒成立,
≥3对任何n∈N*恒成立,∴m≥1,
故选A.
点评:本题考查数列与不等式的综合运用,解题时要认真审题,合理猜想,并用数学归纳法证明猜想.注意等价转化思想的合理运用.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目