题目内容
如果实数x,y满足x2+y2=4,那么3y-4x的最大值是________.
10
分析:可设出圆x2+y2=4参数方程,转化为三角函数,利用三角函数的有界性求最值.
解答:圆x2+y2=4参数方程是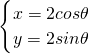 ,θ∈R
,θ∈R
则3y-4x=6sinθ-8cosθ=10sin(θ+∅)
∵θ∈R
∴-10≤10sin(θ+∅)≤10
∴-10≤3y-4x≤10
∴3y-4x的最大值为10
故答案为:10.
点评:此类题常用圆的标准方程将求最值的问题转化到三角函数中用三角函数的有界性求最值.
分析:可设出圆x2+y2=4参数方程,转化为三角函数,利用三角函数的有界性求最值.
解答:圆x2+y2=4参数方程是
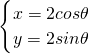 ,θ∈R
,θ∈R则3y-4x=6sinθ-8cosθ=10sin(θ+∅)
∵θ∈R
∴-10≤10sin(θ+∅)≤10
∴-10≤3y-4x≤10
∴3y-4x的最大值为10
故答案为:10.
点评:此类题常用圆的标准方程将求最值的问题转化到三角函数中用三角函数的有界性求最值.

练习册系列答案
相关题目