题目内容

已知点A（4，y0）为抛物线y2=8x上的一点，F为该抛物线的焦点，则|AF|=（　　）
分析：由题意可得抛物线的焦点和准线，而|AF|等于点A到准线的距离d=|4-（-2）|，计算可得．
解答：解：由题意可得抛物线y2=8x的焦点为F（2，0），准线的方程为x=-2，
由抛物线的定义可知|AF|等于点A到准线的距离d，
而d=|4-（-2）|=6，故|AF|=6
故选B
点评：本题考查抛物线的定义，把距离转化来求解是解决的关键，属中档题．
练习册系列答案
相关题目
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率e=
3
2
，连接椭圆的四个顶点得到的菱形的面积为4．
（Ⅰ）求椭圆的方程；
（Ⅱ）设直线l与椭圆相交于不同的两点A、B，已知点A的坐标为（-a，0）．
（i）若|AB|=
4
2
5
，求直线l的倾斜角；
（ii）若点Q（0，y0）在线段AB的垂直平分线上，且
QA
•
QB
=4．求y0的值．
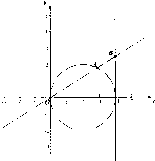精英家教网已知点A（x1，y1）在圆（x-2）2+y2=4上运动，点A不与（0，0）重合，点B（4，y0）在直线x=4上运动，动点M（x，y）满足
OM
∥
OB
，
OM
=
AB
．动点M的轨迹C的方程为F（x，y）=0．
（1）试用点M的坐标x，y表示y0，x1，y1；
（2）求动点M的轨迹方程F（x，y）=0；
（3）以下给出曲线C的五个方面的性质，请你选择其中的三个方面进行研究，并说明理由．（若你研究的方面多于三个，我们将只对试卷解答中的前三项予以评分）
①对称性；
②顶点坐标（定义：曲线与其对称轴的交点称为该曲线的顶点）；
③图形范围；
④渐近线；
⑤对方程F（x，y）=0，当y≥0时，函数y=f（x）的单调性．
（2012•惠州模拟）已知椭圆
x2
a2
+ 
y2
b2
=1(a＞b＞0)的离心率e=
3
2
，连接椭圆的四个顶点得到的菱形的面积为4．
（1）求椭圆的方程；
（2）设直线l与椭圆相交于不同的两点A，B，已知点A的坐标为（-a，0），点Q（0，y0）在线段AB的垂直平分线上，且
QA
• 
QB
=4，求y0的值．
一条双曲线
x2
4
-y2=1的左、右顶点分别为A1，A2，点M（x1，y1），N（x1，-y1）是双曲线上不同的两个动点．
（1）求直线A1M与A2N交点的轨迹E的方程式；
（2）设直线l与曲线E相交于不同的两点A，B，已知点A的坐标为（-2，0），若点Q（0，y0）在线段AB的垂直平分线上，且
QA
•
QB
=4．求y0的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网