题目内容

已知函数f(x)＝mx2＋(m－3)x＋1的图象与x轴的交点至少有一个在原点右侧，则实数m的取值范围是

[　　]

A．(0，1]

B．(0，1)

C．(－∞，1)

D．(－∞，1]

答案：D
解析：

　　解法一：取m＝0有f(x)＝－3x＋1的根x＝＞0，即m＝0应符合题设，所以排除A、B．

　　当m＝1时，f(x)＝x2－2x＋1＝(x－1)2，它的根是x＝1符合要求，排除C，故选D．

　　解法二：直接法．

　　∵f(0)＝1，∴(1)当m＜0时，必成立，排除A、B．

　　(2)当m＞0时，要使与x轴的交点至少有一个在原点的右侧，则

　　∴0＜m≤1．

　　(3)当m＝0时根为x＝＞0．故选D．


练习册系列答案
相关题目

已知函数f(x)＝m－|x－2|，m∈R，且f(x＋2)≥0的解集为[－1,1]．

（1）求m的值；

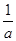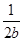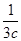（2）若a，b，c∈R＋，且＋＋＝m，求证：a＋2b＋3c≥9.

 

已知函数f(x)＝(m，n∈R)在x＝1处取到极值2.

(1)求f(x)的解析式；

(2)设函数g(x)＝ax－lnx.若对任意的x1∈[，2]，总存在唯一的x2∈[，e](e为自然对数的底)，使得g(x2)＝f(x1)，求实数a的取值范围．

 

 

 

（本小题满分12分）

已知函数f(x)＝m·2x＋t的图象经过点A(1,1)、B(2,3)及C(n，Sn)，Sn为数列{an}的前n项和，n∈N*.

(1)求Sn及an；

(2)若数列{cn}满足cn＝6nan－n，求数列{cn}的前n项和Tn.

 

（本小题满分12分）

已知函数f(x)＝m·2x＋t的图象经过点A(1,1)、B(2,3)及C(n，Sn)，Sn为数列{an}的前n项和，n∈N*.

(1)求Sn及an；

(2)若数列{cn}满足cn＝6nan－n，求数列{cn}的前n项和Tn.

 

已知函数f(x)＝(m，n∈R)在x＝1处取到极值2.

(1)求f(x)的解析式；

(2)设函数g(x)＝ax－lnx.若对任意的x1∈[，2]，总存在唯一的x2∈[，e](e为自然对数的底)，使得g(x2)＝f(x1)，求实数a的取值范围．

 

 

 

 

 

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网