题目内容
已知函数f(x)=x2+(1-m)x-m(1)若m∈R,解不等式f(x)<0;
(2)若m=2,解不等式
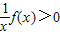 .
.
【答案】分析:(1)利用不等式的性质解不等式.(2)利用分式不等式的解法求不等式.
解答:解:(1)因为f(x)=x2+(1-m)x-m,若f(x)<0.
即为x2+(1-m)x-m<0,
所以(x+1)(x-m)<0.
当m>-1时,不等式的解为:-1<x<m,即不等式的解集为(-1,m).
当m<-1时,不等式的解为:m<x<-1,即不等式的解集为(m,-1).
当m=-1时,不等式的解集为:空集-----------------------------(6分)
(2)当m=2时,不等式化为: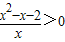 即为:
即为: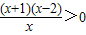
∴原不等式的解集:-1<x<0或x>2,
即不等式的解集为{x|:-1<x<0或x>2}----------------------(14分)
点评:本题主要考查了一元二次不等式的解法,要求熟练掌握.
解答:解:(1)因为f(x)=x2+(1-m)x-m,若f(x)<0.
即为x2+(1-m)x-m<0,
所以(x+1)(x-m)<0.
当m>-1时,不等式的解为:-1<x<m,即不等式的解集为(-1,m).
当m<-1时,不等式的解为:m<x<-1,即不等式的解集为(m,-1).
当m=-1时,不等式的解集为:空集-----------------------------(6分)
(2)当m=2时,不等式化为:
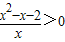 即为:
即为: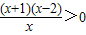
∴原不等式的解集:-1<x<0或x>2,
即不等式的解集为{x|:-1<x<0或x>2}----------------------(14分)
点评:本题主要考查了一元二次不等式的解法,要求熟练掌握.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|