题目内容
数列中,an>0,an≠1,且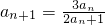 (n∈N*).
(n∈N*).
(1)证明:an≠an+1;
(2)若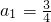 ,计算a2,a3,a4的值,并求出数列的通项公式.
,计算a2,a3,a4的值,并求出数列的通项公式.
解:(1)若an=an+1,即 ,得an=0或an=1与题设矛盾,
,得an=0或an=1与题设矛盾,
∴an≠an+1…(6分)
(2) ,
, ,
, …(8分)
…(8分)
由 ,得
,得 ,
,
∴数列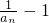 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列,
∴ ,得
,得 …(14分)
…(14分)
分析:(1)采用反证法证明,先假设两种相等,代入已知的等式中即可求出an的值为常数0或1,进而得到此数列为是0或1的常数列,与已知a1>0,a1≠1矛盾,所以假设错误,两种不相等;
(2)把n=1及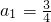 ,代入已知的等式即可求出a2的值,把n=2及a2的值代入已知的等式即可求出a3的值,把n=3及a3的值代入已知等式即可求出a4的值;且
,代入已知的等式即可求出a2的值,把n=2及a2的值代入已知的等式即可求出a3的值,把n=3及a3的值代入已知等式即可求出a4的值;且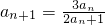 化简成
化简成 进而得到
进而得到 ,从而判断数列
,从而判断数列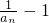 是等比数列,即可得到这个数列的通项公式an.
是等比数列,即可得到这个数列的通项公式an.
点评:此题考查数列的递推式,此题利用反证法对命题进行证明,是一道中档题.
 ,得an=0或an=1与题设矛盾,
,得an=0或an=1与题设矛盾,∴an≠an+1…(6分)
(2)
 ,
, ,
, …(8分)
…(8分)由
 ,得
,得 ,
,∴数列
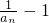 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列,∴
 ,得
,得 …(14分)
…(14分)分析:(1)采用反证法证明,先假设两种相等,代入已知的等式中即可求出an的值为常数0或1,进而得到此数列为是0或1的常数列,与已知a1>0,a1≠1矛盾,所以假设错误,两种不相等;
(2)把n=1及
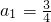 ,代入已知的等式即可求出a2的值,把n=2及a2的值代入已知的等式即可求出a3的值,把n=3及a3的值代入已知等式即可求出a4的值;且
,代入已知的等式即可求出a2的值,把n=2及a2的值代入已知的等式即可求出a3的值,把n=3及a3的值代入已知等式即可求出a4的值;且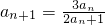 化简成
化简成 进而得到
进而得到 ,从而判断数列
,从而判断数列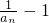 是等比数列,即可得到这个数列的通项公式an.
是等比数列,即可得到这个数列的通项公式an.点评:此题考查数列的递推式,此题利用反证法对命题进行证明,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
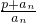 成等比数列.
成等比数列.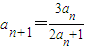 (n∈N*).
(n∈N*).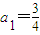 ,计算a2,a3,a4的值,并求出数列的通项公式;
,计算a2,a3,a4的值,并求出数列的通项公式;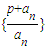 成等比数列.
成等比数列.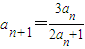 (n∈N*).
(n∈N*).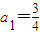 ,计算a2,a3,a4的值,并求出数列的通项公式;
,计算a2,a3,a4的值,并求出数列的通项公式; 成等比数列.
成等比数列.