题目内容

给出函数f(x)=
(
1
3
)x，x≥4
f(x+1)，x＜4
，则f（log34）=
1
108
1
108
．
分析：先判断出1＜
log
4
3
＜2，再由代入对应的关系式，并让自变量连续加1三次，直到log34+3＞4代入第一个解析式，根据“a
log
N
a
=N”和指数幂的运算法则进行求值．
解答：解：∵1＜
log
4
3
＜2，
∴f（log34）=f（log34+1）=f（log34+2）=f（log34+3），
∵log34+3＞4，
∴f（log34）=f（log34+3）=(
1
3
)
log
4
3
+3=3
iog
1
4
3
×(
1
3
)3=
1
4
×
1
27
=
1
108
，
故答案为：
1
108
．
点评：本题考查了分段函数求值，需要确定自变量的范围，再代入对应的解析式进行求解．
练习册系列答案
相关题目
给出函数f(x)=
(
1
2
)x
  x≥3
f(x+1)
 x＜3
，则f（log23）=
1
12
1
12
．
一次研究性课堂上，老师给出函数f(x)=
x
1+|x|
(x∈R)，三位同学在研究此函数时给出以下命题：
①函数f（x）的值域为[-1，1]；     
②若x1≠x2，则一定有f（x1）≠f（x2）；
③对任意的x1，x2∈R，存在x0，使得f（x1）+f（x2）=2f（x0）成立；
④若规定f1(x)=f(x)，fn(x)=f(fn-1(x))， 则 fn(x)=
x
1+n|x|
对任意n∈N*恒成立．
你认为上述命题中正确的是
②③
②③
．（请将正确命题的序号都填上）
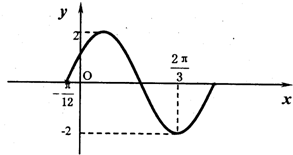精英家教网如图，给出函数f(x)=Acos(ωx+φ)(A＞0，|φ|＜
π2
)图象的一部分，则f（x）的解析式为f（x）=
 
．
一次研究性课堂上，老师给出函数f(x)=
x
1+|x|
(x∈R)，三位同学甲、乙、丙在研究此函数时分别给出命题：
①函数f（x）的值域为(-
1
2
，
1
2
)；
②若x1≠x2，则一定有f（x1）≠f（x2）；
③若规定f1(x)=f(x)，fn(x)=f(fn-1(x))， 则 fn(x)=
x
1+n|x|
对任意n∈N*恒成立．
你认为上述三个命题中正确的是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网