题目内容
若向量
=（x，6）（x∈R），则“||=10”是“x=8”的
- A.充分而不必要条件
- B.必要而不充分条件
- C.充要条件
- D.既不充分又不必要条件
B
分析：利用向量模的平方等于向量的平方列出方程求出x的值，判断出前者成立不能推出后者；反之利用向量模的坐标公式判断出后者成立能推出前者成立，利用充要条件的定义得到结论．
解答：由
得
得x2+36=100得x=±8
反之，当x=8即
则
∴是“x=8”的必要而不充分条件
故选B
点评：判断一个命题是另一个命题的什么条件，一般先化简各个命题，再利用充要条件的定义进行判断．
分析：利用向量模的平方等于向量的平方列出方程求出x的值，判断出前者成立不能推出后者；反之利用向量模的坐标公式判断出后者成立能推出前者成立，利用充要条件的定义得到结论．
解答：由
得得x2+36=100得x=±8反之，当x=8即
则∴
是“x=8”的必要而不充分条件故选B
点评：判断一个命题是另一个命题的什么条件，一般先化简各个命题，再利用充要条件的定义进行判断．
练习册系列答案
相关题目
若向量
=（x-1，2），
=（4，y）相互垂直，则9x+3y的最小值为（ ）
| a |
| b |
| A、12 | ||
B、2
| ||
C、3
| ||
| D、6 |
若向量
=（x，6）（x∈R），则“|
|=10”是“x=8”的（ ）
| a |
| a |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
，
=（x，6），若向量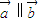
，则实数x的值为 ．