Question

 [2012·湖南卷] 如图1－7，在四棱锥P－ABCD中，PA⊥平面ABCD，底面ABCD是等腰梯形，AD∥BC，AC⊥BD.

(1)证明：BD⊥PC；

(2)若AD＝4，BC＝2，直线PD与平面PAC所成的角为30°，求四棱锥P－ABCD的体积．

Answer 1

解：(1)证明：因为PA⊥平面ABCD，BD⊂平面ABCD，所以PA⊥BD.

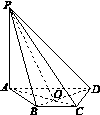
图1－8

又AC⊥BD，PA，AC是平面PAC内的两条相交直线，所以BD⊥平面PAC.

而PC⊂平面PAC，所以BD⊥PC.

(2)设AC和BD相交于点O，连结PO，由(1)知，BD⊥平面PAC，所以∠DPO是直线PD和平面PAC所成的角．从而∠DPO＝30°.

由BD⊥平面PAC，PO⊂平面PAC知，BD⊥PO.

在Rt△POD中，由∠DPO＝30°得PD＝2OD.

因为四边形ABCD为等腰梯形，AC⊥BD，所以△AOD，△BOC均为等腰直角三角形．从而梯形ABCD的高为AD＋BC＝×(4＋2)＝3，于是梯形ABCD的面积S＝×(4＋2)×3＝9.

在等腰直角三角形AOD中，OD＝AD＝2，所以PD＝2OD＝4，PA＝＝4.

故四棱锥P－ABCD的体积为

V＝×S×PA＝×9×4＝12.