题目内容
数列{an}满足a1=1且8an+1an-16an+1+2an+5=0(n≥1).记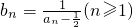 .
.
(Ⅰ)求b1、b2、b3、b4的值;
(Ⅱ)求数列{bn}的通项公式及数列{anbn}的前n项和Sn.
解:法一:
(I)a1=1,故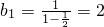 ;
;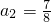 ,
,
故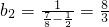 ;
; ,
,
故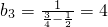 ;
;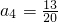 ,
,
故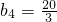 .
.
(II)因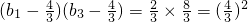 ,
,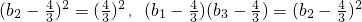
故猜想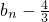 是首项为
是首项为 ,公比q=2的等比数列.
,公比q=2的等比数列.
因an≠2,(否则将an=2代入递推公式会导致矛盾)故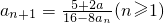 .
.
因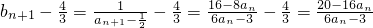 ,
,
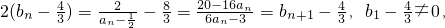
故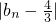 确是公比为q=2的等比数列.
确是公比为q=2的等比数列.
因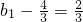 ,故
,故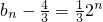 ,
,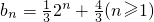 ,
,
由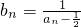 得
得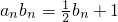 ,
,
故Sn=a1b1+a2b2+…+anbn=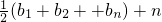 =
=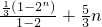 =
=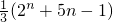
法二:
(Ⅰ)由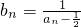 得
得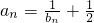 ,代入递推关系8an+1an-16an+1+2an+5=0,
,代入递推关系8an+1an-16an+1+2an+5=0,
整理得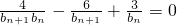 ,即
,即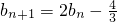 ,
,
由a1=1,有b1=2,所以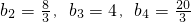 .
.
(Ⅱ)由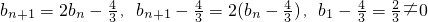 ,
,
所以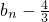 是首项为
是首项为 ,公比q=2的等比数列,
,公比q=2的等比数列,
故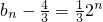 ,即
,即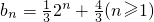 .
.
由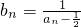 ,得
,得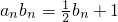 ,
,
故Sn=a1b1+a2b2+…+anbn=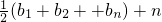 =
=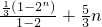 =
=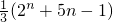 .
.
法三:
(Ⅰ)同解法一
(Ⅱ)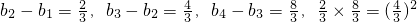 猜想{bn+1-bn}是首项为
猜想{bn+1-bn}是首项为 ,
,
公比q=2的等比数列,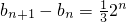
又因an≠2,故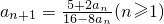 .
.
因此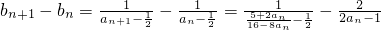 =
=
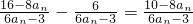 ;
;
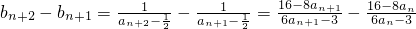 =
=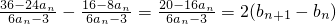 .
.
因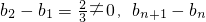 是公比q=2的等比数列,
是公比q=2的等比数列,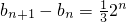 ,
,
从而bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1
=
=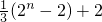
=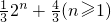 .
.
由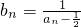 得
得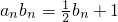 ,
,
故Sn=a1b1+a2b2+…+anbn=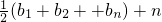 =
=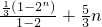 =
=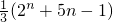 .
.
分析:(法一)(I)由a1结合递推公式可求a2,a3,a4,代入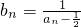 求b1,b2,b3,b4
求b1,b2,b3,b4
(II)先由(I)中求出的b1,b2,b3,b4的值,观察规律可猜想数列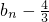 为等比数列,进而可求bn,结合
为等比数列,进而可求bn,结合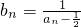 ?
?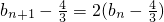 ,从而猜想得以证明,代入求出an•bn,进而求出前n和sn
,从而猜想得以证明,代入求出an•bn,进而求出前n和sn
(法二)(I)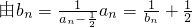 代入递推公式可得
代入递推公式可得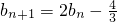 ,代入可求b1,b2,b3,b4
,代入可求b1,b2,b3,b4
(II)利用(I)中的递推关系个构造数列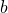 为等比数列,从而可求bn,sn
为等比数列,从而可求bn,sn
(法三)(I)同法一
(II)先由(I)中求出的b1,b2,b3,b4的值,观察规律可猜想数列bn+1-bn为等比数列,仿照法一再证明猜想,根据求通项的方法求bn,进一步求sn
点评:本题考查了数列的综合运用:递推关系的运用,构造等比求数列通项,累加求通项,归纳推理的运用,综合考查了考生的推理运算能力.
(I)a1=1,故
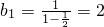 ;
;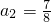 ,
,故
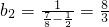 ;
; ,
,故
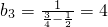 ;
;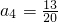 ,
,故
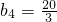 .
.(II)因
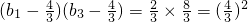 ,
,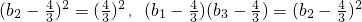
故猜想
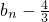 是首项为
是首项为 ,公比q=2的等比数列.
,公比q=2的等比数列.因an≠2,(否则将an=2代入递推公式会导致矛盾)故
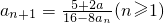 .
.因
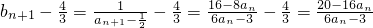 ,
,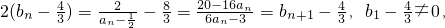
故
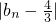 确是公比为q=2的等比数列.
确是公比为q=2的等比数列.因
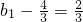 ,故
,故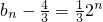 ,
,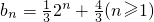 ,
,由
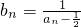 得
得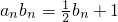 ,
,故Sn=a1b1+a2b2+…+anbn=
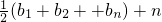 =
=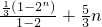 =
=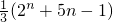
法二:
(Ⅰ)由
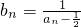 得
得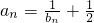 ,代入递推关系8an+1an-16an+1+2an+5=0,
,代入递推关系8an+1an-16an+1+2an+5=0,整理得
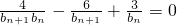 ,即
,即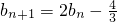 ,
,由a1=1,有b1=2,所以
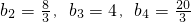 .
.(Ⅱ)由
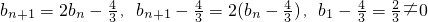 ,
,所以
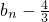 是首项为
是首项为 ,公比q=2的等比数列,
,公比q=2的等比数列,故
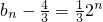 ,即
,即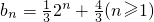 .
.由
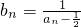 ,得
,得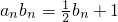 ,
,故Sn=a1b1+a2b2+…+anbn=
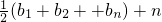 =
=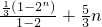 =
=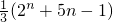 .
.法三:
(Ⅰ)同解法一
(Ⅱ)
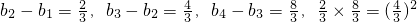 猜想{bn+1-bn}是首项为
猜想{bn+1-bn}是首项为 ,
,公比q=2的等比数列,
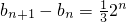
又因an≠2,故
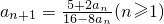 .
.因此
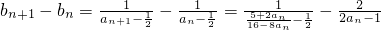 =
=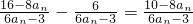 ;
;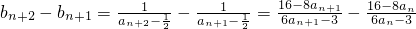 =
=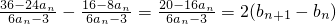 .
.因
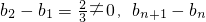 是公比q=2的等比数列,
是公比q=2的等比数列,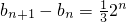 ,
,从而bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1
=

=
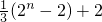
=
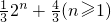 .
.由
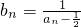 得
得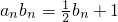 ,
,故Sn=a1b1+a2b2+…+anbn=
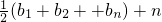 =
=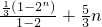 =
=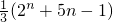 .
.分析:(法一)(I)由a1结合递推公式可求a2,a3,a4,代入
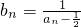 求b1,b2,b3,b4
求b1,b2,b3,b4(II)先由(I)中求出的b1,b2,b3,b4的值,观察规律可猜想数列
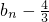 为等比数列,进而可求bn,结合
为等比数列,进而可求bn,结合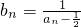 ?
?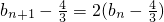 ,从而猜想得以证明,代入求出an•bn,进而求出前n和sn
,从而猜想得以证明,代入求出an•bn,进而求出前n和sn(法二)(I)
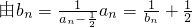 代入递推公式可得
代入递推公式可得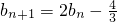 ,代入可求b1,b2,b3,b4
,代入可求b1,b2,b3,b4(II)利用(I)中的递推关系个构造数列
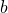 为等比数列,从而可求bn,sn
为等比数列,从而可求bn,sn(法三)(I)同法一
(II)先由(I)中求出的b1,b2,b3,b4的值,观察规律可猜想数列bn+1-bn为等比数列,仿照法一再证明猜想,根据求通项的方法求bn,进一步求sn
点评:本题考查了数列的综合运用:递推关系的运用,构造等比求数列通项,累加求通项,归纳推理的运用,综合考查了考生的推理运算能力.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目