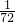题目内容
函数 的最大值是
的最大值是
- A.

- B.

- C.

- D.

D
分析:先将y=
 化成sinx-ycosx=4y+3,再利用三角函数的和角公式化成:
化成sinx-ycosx=4y+3,再利用三角函数的和角公式化成: sin(x+θ)=4y-3,最后利用三角函数的有界性即可求得值域.
sin(x+θ)=4y-3,最后利用三角函数的有界性即可求得值域.
解答:∵ ,
,
∴sinx-3=4y+ycosx,
∴sinx-ycosx=4y+3,
即: sin(x+θ)=4y+3,
sin(x+θ)=4y+3,
∵- ≤
≤ sin(x+θ)≤
sin(x+θ)≤ ,
,
∴- ≤4y+3≤
≤4y+3≤ ,
,
解得:y∈[ ].
].
故选D.
点评:本题以三角函数为载体考查分式函数的值域,属于求三角函数的最值问题,属于基本题.
分析:先将y=

 化成sinx-ycosx=4y+3,再利用三角函数的和角公式化成:
化成sinx-ycosx=4y+3,再利用三角函数的和角公式化成: sin(x+θ)=4y-3,最后利用三角函数的有界性即可求得值域.
sin(x+θ)=4y-3,最后利用三角函数的有界性即可求得值域.解答:∵
 ,
,∴sinx-3=4y+ycosx,
∴sinx-ycosx=4y+3,
即:
 sin(x+θ)=4y+3,
sin(x+θ)=4y+3,∵-
 ≤
≤ sin(x+θ)≤
sin(x+θ)≤ ,
,∴-
 ≤4y+3≤
≤4y+3≤ ,
,解得:y∈[
 ].
].故选D.
点评:本题以三角函数为载体考查分式函数的值域,属于求三角函数的最值问题,属于基本题.

练习册系列答案
相关题目
 的最大值是
的最大值是


 的最大值是( )
的最大值是( ) B.
B. C.
C. D.
D.
 满足约束条件
满足约束条件 则目标函数
则目标函数 的最大值是
的最大值是 B.
B.  C.
C.  D.
D. 
 的最大值是
的最大值是 B
l C.
O
D.
B
l C.
O
D.
 的最大值是
的最大值是