题目内容
9.已知an=(2n-1)($\frac{1}{2}$)n,求前n项和Sn.分析 运用数列的求和方法:错位相减法,结合等比数列的求和公式,化简计算即可得到所求.
解答 解:前n项和Sn=1•$\frac{1}{2}$+3•$\frac{1}{4}$+5•$\frac{1}{8}$+…+(2n-1)•($\frac{1}{2}$)n,①
$\frac{1}{2}$Sn=1•$\frac{1}{4}$+3•$\frac{1}{8}$+5•$\frac{1}{16}$+…+(2n-1)•($\frac{1}{2}$)n+1,②
①-②可得,$\frac{1}{2}$Sn=$\frac{1}{2}$+2[$\frac{1}{4}$+$\frac{1}{8}$+…+($\frac{1}{2}$)n]-(2n-1)•($\frac{1}{2}$)n+1
=$\frac{1}{2}$+2•$\frac{\frac{1}{4}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$-(2n-1)•($\frac{1}{2}$)n+1
化简可得,Sn=3-(2n+3)•($\frac{1}{2}$)n.
点评 本题考查数列的求和:错位相减法,同时考查等比数列的求和公式的运用,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知数列{an}的前n项的乘积为Tn=3${\;}^{{n}^{2}}$(n∈N*),则数列{an}的前n项的和为( )
| A. | $\frac{3}{2}$(3n-1) | B. | $\frac{9}{2}$(3n-1) | C. | $\frac{3}{8}$(9n-1) | D. | $\frac{9}{8}$(9n-1) |
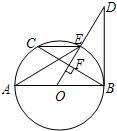 如图所示,AB是⊙O的直径,OD垂直于弦BC于点F,且交⊙O于点E,若BD是⊙O的切线且∠BDO=∠EAB.
如图所示,AB是⊙O的直径,OD垂直于弦BC于点F,且交⊙O于点E,若BD是⊙O的切线且∠BDO=∠EAB.