题目内容
已知函数 ,
,
(1)求函数f(x)的周期及最大值;
(2)若将f(x)的图象向左平移 后,再将所有点的横坐标缩小到原来的
后,再将所有点的横坐标缩小到原来的 倍,得到函数g(x)的图象,求函数g(x)在区间
倍,得到函数g(x)的图象,求函数g(x)在区间 上的值域.
上的值域.
解:
= (1+cos2x)-sin2x-
(1+cos2x)-sin2x-
= cos2x-sin2x
cos2x-sin2x
=2cos(2x+ ),
),
(1)∵ω=2,∴T= =π;
=π;
又cos(2x+ )∈[-1,1],
)∈[-1,1],
∴函数f(x)的最大值为2;
(2)将函数f(x)的图象向左平移 个单位后,
个单位后,
得到函数f(x)=2cos(2x+ +
+ )=-2sin(2x+
)=-2sin(2x+ ),
),
再将所有点的横坐标缩小到原来的 倍,得到函数g(x)的图象,
倍,得到函数g(x)的图象,
则g(x)的解析式为: ,
,
∵x∈ ,∴4x+
,∴4x+ ∈[-
∈[- ,
, ],
],
∴sin(4x+ )∈[-
)∈[- ,1],
,1],
则 的值域为[-2,1].
的值域为[-2,1].
分析:把函数解析式第一项利用二倍角的余弦函数公式化简,第二项利用二倍角的正弦函数公式化简,整理后提取2,再利用两角和与差的余弦函数公式及特殊角的三角函数值化为一个角的余弦函数,
(1)找出ω的值,代入周期公式T=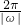 即可求出函数的最小正周期,再根据正弦函数的值域可得出函数的最大值;
即可求出函数的最小正周期,再根据正弦函数的值域可得出函数的最大值;
(2)根据三角函数图象的平移规律:左加右减,给x加上 ,整理后,再把ω变为2ω,使其所有点的横坐标缩小到原来的
,整理后,再把ω变为2ω,使其所有点的横坐标缩小到原来的 倍,确定出g(x)的解析式,由x的范围求出g(x)中角度的范围,利用正弦函数的值域即可得到g(x)的值域.
倍,确定出g(x)的解析式,由x的范围求出g(x)中角度的范围,利用正弦函数的值域即可得到g(x)的值域.
点评:此题考查了三角函数的周期性及其求法,涉及的知识有:二倍角的正弦、余弦函数公式,两角和与差的余弦函数公式,正弦函数的定义域和值域,三角函数图象的平移与变换规律,以及特殊角的三角函数值,其中利用三角函数的恒等变换把函数解析式化为一个角的余弦函数是解本题的关键.

=
 (1+cos2x)-sin2x-
(1+cos2x)-sin2x-
=
 cos2x-sin2x
cos2x-sin2x=2cos(2x+
 ),
),(1)∵ω=2,∴T=
 =π;
=π;又cos(2x+
 )∈[-1,1],
)∈[-1,1],∴函数f(x)的最大值为2;
(2)将函数f(x)的图象向左平移
 个单位后,
个单位后,得到函数f(x)=2cos(2x+
 +
+ )=-2sin(2x+
)=-2sin(2x+ ),
),再将所有点的横坐标缩小到原来的
 倍,得到函数g(x)的图象,
倍,得到函数g(x)的图象,则g(x)的解析式为:
 ,
,∵x∈
 ,∴4x+
,∴4x+ ∈[-
∈[- ,
, ],
],∴sin(4x+
 )∈[-
)∈[- ,1],
,1],则
 的值域为[-2,1].
的值域为[-2,1].分析:把函数解析式第一项利用二倍角的余弦函数公式化简,第二项利用二倍角的正弦函数公式化简,整理后提取2,再利用两角和与差的余弦函数公式及特殊角的三角函数值化为一个角的余弦函数,
(1)找出ω的值,代入周期公式T=
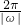 即可求出函数的最小正周期,再根据正弦函数的值域可得出函数的最大值;
即可求出函数的最小正周期,再根据正弦函数的值域可得出函数的最大值;(2)根据三角函数图象的平移规律:左加右减,给x加上
 ,整理后,再把ω变为2ω,使其所有点的横坐标缩小到原来的
,整理后,再把ω变为2ω,使其所有点的横坐标缩小到原来的 倍,确定出g(x)的解析式,由x的范围求出g(x)中角度的范围,利用正弦函数的值域即可得到g(x)的值域.
倍,确定出g(x)的解析式,由x的范围求出g(x)中角度的范围,利用正弦函数的值域即可得到g(x)的值域.点评:此题考查了三角函数的周期性及其求法,涉及的知识有:二倍角的正弦、余弦函数公式,两角和与差的余弦函数公式,正弦函数的定义域和值域,三角函数图象的平移与变换规律,以及特殊角的三角函数值,其中利用三角函数的恒等变换把函数解析式化为一个角的余弦函数是解本题的关键.

练习册系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.