题目内容
((本小题满分14分)
已知两点M(-1,0),N(1,0),且点P使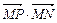 ,
,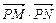 ,
,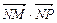 成公差小于零的等差数列。
成公差小于零的等差数列。
(1)点P的轨迹是什么曲线?
(2)若点P的坐标为(x0,y0),记为θ为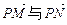 的夹角,求tanθ.
的夹角,求tanθ.
已知两点M(-1,0),N(1,0),且点P使
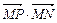 ,
,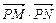 ,
,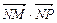 成公差小于零的等差数列。
成公差小于零的等差数列。(1)点P的轨迹是什么曲线?
(2)若点P的坐标为(x0,y0),记为θ为
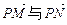 的夹角,求tanθ.
的夹角,求tanθ.解:(1)记P(x,y),由M(-1,0),N( 1,0)得
1,0)得
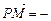
 =(-1-x,-y),
=(-1-x,-y),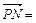
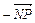 =(1-x,-y),
=(1-x,-y),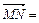
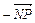 =(2,0)
=(2,0)
所以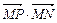 =2(1+x),
=2(1+x),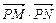 = x2+y2-1,
= x2+y2-1,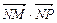 =2(1-x)……3分
=2(1-x)……3分
于是,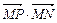 ,
,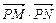 ,
,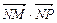 是公差小于零的等差数列,等价于
是公差小于零的等差数列,等价于
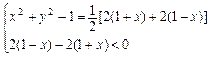 ,即
,即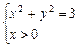 ,
,
所以,点P的轨迹是以原点为圆心,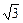 为半径的右半圆.…………………6分
为半径的右半圆.…………………6分
(2)点P的坐标为(x0,y0).
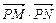 =
=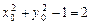 ,
,
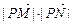 =
=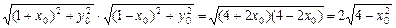 ,
,
所以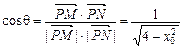 .………………………………………9分
.………………………………………9分
因为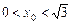 ,所以
,所以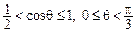 ,…………………………11分
,…………………………11分
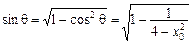 ,
,
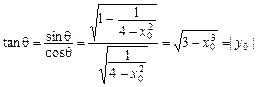 .……………………………14分
.……………………………14分
 1,0)得
1,0)得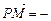
 =(-1-x,-y),
=(-1-x,-y),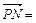
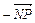 =(1-x,-y),
=(1-x,-y),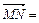
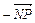 =(2,0)
=(2,0)所以
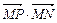 =2(1+x),
=2(1+x),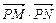 = x2+y2-1,
= x2+y2-1,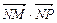 =2(1-x)……3分
=2(1-x)……3分于是,
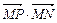 ,
,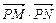 ,
,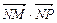 是公差小于零的等差数列,等价于
是公差小于零的等差数列,等价于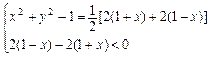 ,即
,即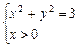 ,
,所以,点P的轨迹是以原点为圆心,
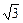 为半径的右半圆.…………………6分
为半径的右半圆.…………………6分(2)点P的坐标为(x0,y0).
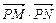 =
=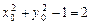 ,
,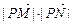 =
=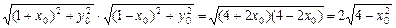 ,
,所以
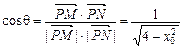 .………………………………………9分
.………………………………………9分因为
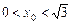 ,所以
,所以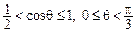 ,…………………………11分
,…………………………11分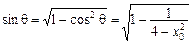 ,
,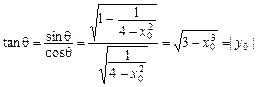 .……………………………14分
.……………………………14分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
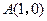 、
、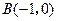 ,已知
,已知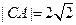 ,
,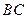 的垂直平分线
的垂直平分线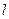 交
交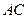 于
于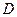 ,当点
,当点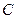 为动点时,点
为动点时,点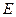 .
.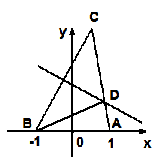
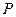 为
为 为坐标原点,曲线
为坐标原点,曲线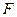 ,求
,求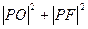 的最小值.
的最小值.
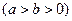 的离心率为
的离心率为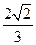 ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为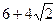 .
.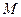 的方程;
的方程;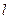 与椭圆
与椭圆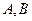 两点,且以
两点,且以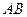 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点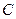 ,
,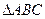 面积的最大值.
面积的最大值.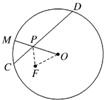
 )
)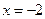 的距离比它到点F
的距离比它到点F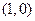 的距离大1,
的距离大1,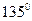 的直线交曲线C于A、B两点,求AB的长
的直线交曲线C于A、B两点,求AB的长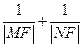 为定值
为定值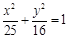 的离心率为
的离心率为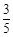
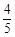
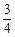
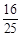
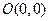 、
、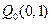 和
和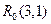 ,记
,记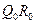 的中点为
的中点为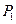 ,取
,取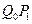 和
和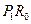 中的一条,记其端点为
中的一条,记其端点为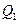 、
、 ,使之满足
,使之满足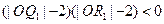 ;记
;记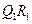 的中点为
的中点为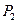 ,取
,取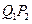 和
和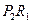 中的一条,记其端点为
中的一条,记其端点为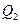 、
、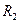 ,使之满足
,使之满足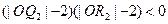 ;依次下去,得到点
;依次下去,得到点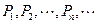 ,则
,则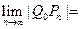 。
。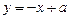 与曲线
与曲线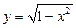 有两个交点,则
有两个交点,则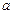 的取值范围是 .
的取值范围是 .