题目内容
 如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1、x2,其中-2<x1<-1,0<x2<1.下列结论:①4a-2b+c<0;②2a-b<0;③a<-1;④b2+8a>4ac.其中正确结论的序号是
如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1、x2,其中-2<x1<-1,0<x2<1.下列结论:①4a-2b+c<0;②2a-b<0;③a<-1;④b2+8a>4ac.其中正确结论的序号是①②③④
①②③④
.分析:首先根据抛物线的开口方向可得到a<0,抛物线交y轴于正半轴,则c>0,而抛物线与x轴的交点中,-2<x1<-1、0<x2<1说明抛物线的对称轴在-1~0之间,即x=-
>-1,可根据这些条件以及函数图象上一些特殊点的坐标来进行判断.
| b |
| 2a |
解答:解:由图知:抛物线的开口向下,则a<0;抛物线的对称轴x=-
>-1,且c>0;
①由图可得:当x=-2时,y<0,即4a-2b+c<0,故①正确;
②已知x=-
>-1,且a<0,所以2a-b<0,故②正确;
③已知抛物线经过(-1,2),即a-b+c=2(1),由图知:当x=1时,y<0,即a+b+c<0(2),
由①知:4a-2b+c<0(3);联立(1)(2),得:a+c<1;联立(1)(3)得:2a-c<-4;
故3a<-3,即a<-1;所以③正确;
④由于抛物线的对称轴大于-1,所以抛物线的顶点纵坐标应该大于2,即:
>2,由于a<0,所以4ac-b2<8a,即b2+8a>4ac,故④正确;
因此正确的结论是①②③④.
故答案为:①②③④.
| b |
| 2a |
①由图可得:当x=-2时,y<0,即4a-2b+c<0,故①正确;
②已知x=-
| b |
| 2a |
③已知抛物线经过(-1,2),即a-b+c=2(1),由图知:当x=1时,y<0,即a+b+c<0(2),
由①知:4a-2b+c<0(3);联立(1)(2),得:a+c<1;联立(1)(3)得:2a-c<-4;
故3a<-3,即a<-1;所以③正确;
④由于抛物线的对称轴大于-1,所以抛物线的顶点纵坐标应该大于2,即:
| 4ac-b2 |
| 4a |
因此正确的结论是①②③④.
故答案为:①②③④.
点评:本题主要考查对二次函数图象与系数的关系,抛物线与x轴的交点,二次函数图象上点的坐标特征等知识点的理解和掌握,能根据图象确定与系数有关的式子的正负是解此题的关键.

练习册系列答案
相关题目
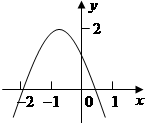 如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2.其中-2<x1<-1,0<x2<1,
如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2.其中-2<x1<-1,0<x2<1, 小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:①ab>0;②a+b+c<0;③b+2c>0;④a-2b+4c>0;⑤
小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:①ab>0;②a+b+c<0;③b+2c>0;④a-2b+4c>0;⑤



