题目内容
已知函数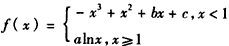 的图象过坐标原点O,且在点(-1,f(-1))处的切线的斜率是-5.
的图象过坐标原点O,且在点(-1,f(-1))处的切线的斜率是-5.
(Ⅰ)求实数b,c的值;
(Ⅱ)求f(x)在区间[-1,2]上的最大值;
(Ⅲ)对任意给定的正实数a,曲线y=f(x)上是否存在两点P,Q,使得△POQ是以O为直角顶点的直角三角形,且此三角形斜边中点在y轴上?说明理由.
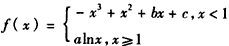 的图象过坐标原点O,且在点(-1,f(-1))处的切线的斜率是-5.
的图象过坐标原点O,且在点(-1,f(-1))处的切线的斜率是-5.(Ⅰ)求实数b,c的值;
(Ⅱ)求f(x)在区间[-1,2]上的最大值;
(Ⅲ)对任意给定的正实数a,曲线y=f(x)上是否存在两点P,Q,使得△POQ是以O为直角顶点的直角三角形,且此三角形斜边中点在y轴上?说明理由.
解:(Ⅰ)当x<1时,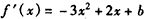 ,
,
依题意,得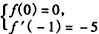 ,即
,即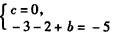 ,
,
解得b=c=0.
(Ⅱ)由(Ⅰ)知,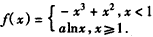 ,
,
①当-1≤x<1时,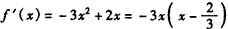 ,
,
令f′(x)=0得x=0或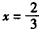 ,
,
x变化时,f′(x),f(x)的变化情况如下表:
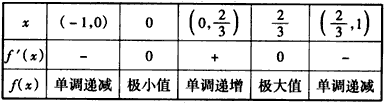
又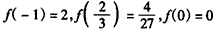 ,
,
∴f(x)在[-1,1)上的最大值为2;
②当1≤x≤2时,f(x)=alnx,
当a≤0时,f(x)≤0;
当a>0时,f(x)在[1,2]上单调递增,
∴f(x)在[1,2]的最大值为aln2;
综上所述,当aln2≤2,即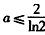 时,f(x)在[-1,2]上的最大值为2;
时,f(x)在[-1,2]上的最大值为2;
当aln2>2,即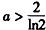 时,f(x)在[-1,2]上的最大值为aln2。
时,f(x)在[-1,2]上的最大值为aln2。
(Ⅲ)假设曲线y=f(x)上存在两点P,Q满足题设要求,则点P,Q只能在y轴的两侧,
不妨设P(t,f(t))(t>0),则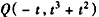 ,显然t≠1,
,显然t≠1,
∵△POQ为直角三角形,
∴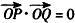 ,即
,即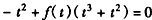 ,①
,①
是否存在P,Q等价于方程①是否有解,
若0<t<1,则f(t)=-t3+t2,代入①式得,-t2+(-t3+t2)(t3+t2)=0,
即t4-t2+1=0,而此方程无实数解,因此t>1,
∴f(t)=alnt,代入①式得,-t2+(alnt)(t3+t2)=0,即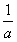 =(t+1)lnt,(*)
=(t+1)lnt,(*)
考察函数h(x)=(x+1)lnx(x≥1),则h′(x)=lnx+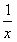 +1>0,
+1>0,
∴h(x)在[1,+∞)上单调递增,
∵t>1,
∴h(t)>h(1)=0,当t→+∞时,h(t)→+∞,
∴h(t)的取值范围为(0,+∞),
∴对于a>0,方程(*)总有解,即方程①总有解,
因此对任意给定的正实数a,曲线y=f(x)上总存在两点P,Q使得△POQ是以点O为直角顶点的直角三角形,且此三角形斜边中点在y轴上。
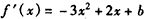 ,
,依题意,得
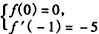 ,即
,即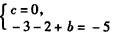 ,
,解得b=c=0.
(Ⅱ)由(Ⅰ)知,
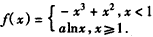 ,
,①当-1≤x<1时,
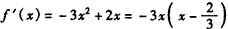 ,
,令f′(x)=0得x=0或
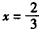 ,
,x变化时,f′(x),f(x)的变化情况如下表:

又
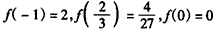 ,
, ∴f(x)在[-1,1)上的最大值为2;
②当1≤x≤2时,f(x)=alnx,
当a≤0时,f(x)≤0;
当a>0时,f(x)在[1,2]上单调递增,
∴f(x)在[1,2]的最大值为aln2;
综上所述,当aln2≤2,即
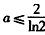 时,f(x)在[-1,2]上的最大值为2;
时,f(x)在[-1,2]上的最大值为2;当aln2>2,即
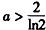 时,f(x)在[-1,2]上的最大值为aln2。
时,f(x)在[-1,2]上的最大值为aln2。(Ⅲ)假设曲线y=f(x)上存在两点P,Q满足题设要求,则点P,Q只能在y轴的两侧,
不妨设P(t,f(t))(t>0),则
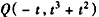 ,显然t≠1,
,显然t≠1,∵△POQ为直角三角形,
∴
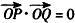 ,即
,即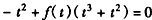 ,①
,① 是否存在P,Q等价于方程①是否有解,
若0<t<1,则f(t)=-t3+t2,代入①式得,-t2+(-t3+t2)(t3+t2)=0,
即t4-t2+1=0,而此方程无实数解,因此t>1,
∴f(t)=alnt,代入①式得,-t2+(alnt)(t3+t2)=0,即
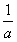 =(t+1)lnt,(*)
=(t+1)lnt,(*) 考察函数h(x)=(x+1)lnx(x≥1),则h′(x)=lnx+
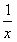 +1>0,
+1>0,∴h(x)在[1,+∞)上单调递增,
∵t>1,
∴h(t)>h(1)=0,当t→+∞时,h(t)→+∞,
∴h(t)的取值范围为(0,+∞),
∴对于a>0,方程(*)总有解,即方程①总有解,
因此对任意给定的正实数a,曲线y=f(x)上总存在两点P,Q使得△POQ是以点O为直角顶点的直角三角形,且此三角形斜边中点在y轴上。

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
已知函数 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点 处的切线的斜率是
处的切线的斜率是 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求 在区间
在区间 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数 ,曲线
,曲线 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上?说明理由.
轴上?说明理由.
【解析】第一问当 时,
时, ,则
,则 。
。
依题意得: ,即
,即 解得
解得
第二问当 时,
时, ,令
,令 得
得 ,结合导数和函数之间的关系得到单调性的判定,得到极值和最值
,结合导数和函数之间的关系得到单调性的判定,得到极值和最值
第三问假设曲线 上存在两点P、Q满足题设要求,则点P、Q只能在
上存在两点P、Q满足题设要求,则点P、Q只能在 轴两侧。
轴两侧。
不妨设 ,则
,则 ,显然
,显然
∵ 是以O为直角顶点的直角三角形,∴
是以O为直角顶点的直角三角形,∴
即 (*)若方程(*)有解,存在满足题设要求的两点P、Q;
(*)若方程(*)有解,存在满足题设要求的两点P、Q;
若方程(*)无解,不存在满足题设要求的两点P、Q.
(Ⅰ)当 时,
时, ,则
,则 。
。
依题意得: ,即
,即 解得
解得
(Ⅱ)由(Ⅰ)知,
①当 时,
时, ,令
,令 得
得
当 变化时,
变化时, 的变化情况如下表:
的变化情况如下表:
|
|
|
0 |
|
|
|
|
|
— |
0 |
+ |
0 |
— |
|
|
|
极小值 |
单调递增 |
极大值 |
|
又 ,
, ,
, 。∴
。∴ 在
在 上的最大值为2.
上的最大值为2.
②当 时,
时,  .当
.当 时,
时,  ,
, 最大值为0;
最大值为0;
当 时,
时,  在
在 上单调递增。∴
上单调递增。∴ 在
在 最大值为
最大值为 。
。
综上,当 时,即
时,即 时,
时, 在区间
在区间 上的最大值为2;
上的最大值为2;
当 时,即
时,即 时,
时, 在区间
在区间 上的最大值为
上的最大值为 。
。
(Ⅲ)假设曲线 上存在两点P、Q满足题设要求,则点P、Q只能在
上存在两点P、Q满足题设要求,则点P、Q只能在 轴两侧。
轴两侧。
不妨设 ,则
,则 ,显然
,显然
∵ 是以O为直角顶点的直角三角形,∴
是以O为直角顶点的直角三角形,∴
即 (*)若方程(*)有解,存在满足题设要求的两点P、Q;
(*)若方程(*)有解,存在满足题设要求的两点P、Q;
若方程(*)无解,不存在满足题设要求的两点P、Q.
若 ,则
,则 代入(*)式得:
代入(*)式得:
即 ,而此方程无解,因此
,而此方程无解,因此 。此时
。此时 ,
,
代入(*)式得:  即
即 (**)
(**)
令
 ,则
,则
∴ 在
在 上单调递增, ∵
上单调递增, ∵  ∴
∴ ,∴
,∴ 的取值范围是
的取值范围是 。
。
∴对于 ,方程(**)总有解,即方程(*)总有解。
,方程(**)总有解,即方程(*)总有解。
因此,对任意给定的正实数 ,曲线
,曲线 上存在两点P、Q,使得
上存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上
轴上
 的图象过坐标原点O,且在点(-1,f(-1))处的切线的斜率是-5.
的图象过坐标原点O,且在点(-1,f(-1))处的切线的斜率是-5. 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点 处的切线的斜率是
处的切线的斜率是 .
. 的值;
的值;  在区间
在区间 上的最大值;
上的最大值; ,曲线
,曲线 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上?说明理由.
轴上?说明理由.




 单调递减
单调递减 的图象过坐标原点O, 且在点
的图象过坐标原点O, 且在点 处的切线的斜率是
处的切线的斜率是 .(1)求实数
.(1)求实数 的值; (2)求
的值; (2)求 在区间
在区间 上的最大值
上的最大值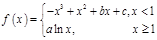 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点 处的切线的斜率是
处的切线的斜率是 5.
5. 的值;
的值; 在区间
在区间 上的最大值;
上的最大值;