题目内容
函数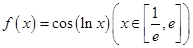 的单调递减区间是 .
的单调递减区间是 .
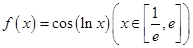 的单调递减区间是 .
的单调递减区间是 .
试题分析:因为
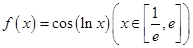 ,所以
,所以 ,
, ,所以函数的单调递减区间是
,所以函数的单调递减区间是 。
。点评:求复合函数的导数的方法步骤:(1)分析清楚复合函数的复合关系,选好中间变量;(2)运用复合函数的求导法则求复合函数的导数,注意分清每次是哪个变量对哪个变量求导数;(3)根据基本函数的导数公式及导数的运算法则,求出各函数的导数,并把中间变量换成自变量的函数。

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
题目内容
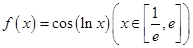 的单调递减区间是 .
的单调递减区间是 .
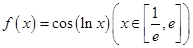 ,所以
,所以 ,
, ,所以函数的单调递减区间是
,所以函数的单调递减区间是 。
。
 天天向上口算本系列答案
天天向上口算本系列答案