题目内容
已知抛物线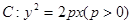 的准线为
的准线为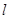 ,焦点为
,焦点为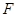 ,圆
,圆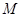 的圆心在
的圆心在 轴的正半轴上,且与
轴的正半轴上,且与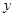 轴相切,过原点
轴相切,过原点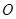 作倾斜角为
作倾斜角为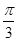 的直线
的直线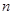 ,交
,交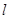 于点
于点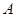 ,交圆
,交圆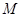 于另一点
于另一点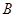 ,且
,且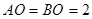
(1)求圆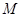 和抛物线C的方程;
和抛物线C的方程;
(2)若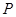 为抛物线C上的动点,求
为抛物线C上的动点,求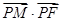 的最小值;
的最小值;
(3)过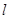 上的动点Q向圆
上的动点Q向圆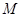 作切线,切点为S,T,
作切线,切点为S,T,
求证:直线ST恒过一个定点,并求该定点的坐标.

【答案】
解:(1)易得 ,
, ,设圆
,设圆 的方程为
的方程为 ,
,
将点 代入得
代入得 ,所以圆
,所以圆 的方程为
的方程为
点 在准线
在准线 上,从而
上,从而 ,抛物线的方程为
,抛物线的方程为
(2)由(1)得 ,设点
,设点 ,则
,则
得 ,
, ,
,
所以
因为 ,所以
,所以 ,即
,即 的最小值为
的最小值为 .
.
(3)设点 ,过点
,过点 的切线长为
的切线长为 ,则以
,则以 为圆心,切线长为半径的圆的方程为
为圆心,切线长为半径的圆的方程为 ,
,
即 ①
①
又圆 的方程为
的方程为 ,即
,即 ②
②
由①②两式相减即得直线 的方程:
的方程:
显然上面直线恒过定点
【解析】略

练习册系列答案
 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
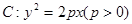 的准线为
的准线为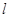 ,焦点为F,
,焦点为F,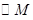 的圆心在
的圆心在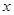 轴的正半轴上,且与
轴的正半轴上,且与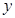 轴相切,过原点O作倾斜角为
轴相切,过原点O作倾斜角为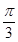 的直线
的直线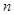 ,交
,交 的最小值;
的最小值;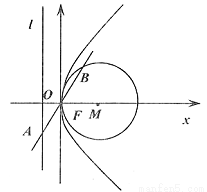
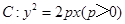 的准线为
的准线为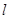 ,过
,过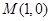 且斜率为
且斜率为 的直线与
的直线与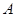 ,与
,与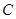 的一个交点为
的一个交点为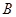 .若
.若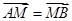 ,则P的值为( )
,则P的值为( ) 的准线为
的准线为 ,过
,过 且斜率为
且斜率为 的
的 ,与
,与 的一个交点为
的一个交点为 .若
.若 ,则
,则
 的准线为
的准线为 ,过
,过 且斜率为
且斜率为 的直线与
的直线与 ,与
,与 的一个交点为
的一个交点为 .若
.若 ,则
,则 .
.