题目内容
(本小题10分)
对于函数f(x)(x![]() )恒有f(ab)=f(a)+f(b)且x>1时f(x)>0 ,f(2)=1
)恒有f(ab)=f(a)+f(b)且x>1时f(x)>0 ,f(2)=1
(1)求f(4)、f(1)、f(-1)的值;
(2)求证f(x)为偶函数;
(3)求证f(x)在(0,+![]() )上是增函数;
)上是增函数;
(4)解不等式f(x![]() -5)<2.
-5)<2.
解:(1)f(4)=2 f(1)=0 f(-1)=0
(2)令a=x,b=-1得f(-x)=f(x)+f(-1)即f(-x)=f(x)
![]() f(x)是偶函数
f(x)是偶函数
(3)设0<![]() <
<![]() 且
且![]() ,
,![]() 任意令
任意令![]() 则f(
则f(![]() )= f(
)= f(![]() )+f(
)+f(![]() )
)
由0<![]() <
<![]() 得
得![]() >1
>1![]() f(
f(![]() )>0
)>0![]() f(
f(![]() )-f(
)-f(![]() )>0
)>0
![]() f(x)在(0,+
f(x)在(0,+![]() )上是函数
)上是函数
(4)由f(4)=2 得f(x![]() -5)<f(4)
-5)<f(4)![]() -4<x
-4<x![]() -5<4
-5<4
![]() 不等式f(x
不等式f(x![]() -5)<2的解集为(-3,-1)
-5)<2的解集为(-3,-1)![]() (1,3)
(1,3)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 与销售额
与销售额 之间有如下的对应数据:
之间有如下的对应数据: 
 中,
中,  分别是
分别是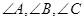 的对边,
的对边, 是方程
是方程 的两个根,且
的两个根,且 .
. 的度数和
的度数和 的长度.
的长度. 的函数
的函数 ,
,
 ,
, ,写出函数
,写出函数 的解析式;
的解析式;  , 其中
, 其中 是常数,且
是常数,且 ,请设计一个定义域为R的函数
,请设计一个定义域为R的函数 及一个
及一个 ,并予以证明.
,并予以证明. ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对 进行如下操作得到:将
进行如下操作得到:将 ).
).
 和
和 (
( ),求
),求 为曲线
为曲线 的递推关系式,并求
的递推关系式,并求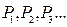 ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对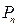 进行如下操作得到:将
进行如下操作得到:将 ).
).
 和
和 (
( ),求
),求 为曲线
为曲线 的递推关系式,并求
的递推关系式,并求