题目内容
【题目】已知二次函数![]()
(1)若函数![]() 是偶函数,求实数
是偶函数,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 且任意
且任意![]() 都有
都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,求
,求![]() 在
在![]() 上的最小值
上的最小值![]() 。
。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)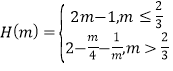 .
.
【解析】
(1)偶函数f(﹣x)=f(x)x2+mx+1=x2﹣mx+1,可求实数m的取值范围;
(2)m∈[﹣1,3],g(x)=f(x)+(2m﹣1)x﹣9=x2+(m﹣1)x﹣8≤0恒成立![]() ,解之即得实数x的取值范围;
,解之即得实数x的取值范围;
(3)若函数h(x)=f(x)﹣(1﹣m)x2+2x=mx2+(2﹣m)x+1,分![]() 、m
、m![]() 、当m<0及m=0四类讨论,即可求得函数y=h(x)在x∈[﹣1,1]的最小值H(m).
、当m<0及m=0四类讨论,即可求得函数y=h(x)在x∈[﹣1,1]的最小值H(m).
(1)函数![]() 是偶函数,
是偶函数,![]()
![]() ,
,
![]()
(2)![]()
![]() 都有
都有![]() 恒成立
恒成立
![]() ,
,![]()
![]() 实数
实数![]() 的取值范围是
的取值范围是![]()
(3)![]()
①当![]() 时,函数
时,函数![]() 对称轴
对称轴![]()
![]() 函数
函数![]() 在
在![]() 上的最小值
上的最小值![]()
②当![]() 时,函数
时,函数![]() 对称轴
对称轴![]()
![]() 函数
函数![]() 在
在![]() 上的最小值
上的最小值
![]()
③当![]() 时,函数
时,函数![]() 的对称轴
的对称轴![]()
![]() 函数
函数![]() 在
在![]() 上的最小值
上的最小值![]()
④当![]() 时,函数
时,函数![]()
![]() 函数
函数![]() 在
在![]() 上的最小值
上的最小值![]()
综上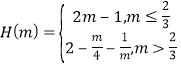

练习册系列答案
相关题目


