题目内容
已知![]() 函数
函数![]() 的一个零点为x=1,另外两个零点可分别作为一个椭圆、一个双曲线的离心率.
的一个零点为x=1,另外两个零点可分别作为一个椭圆、一个双曲线的离心率.
(1)求a+b+c;
(2)求![]() 的取值范围.
的取值范围.
解:(1)由f(1)=0,∴a+b+c=-1.
(2)由c=-1-a-b,
∴f(x)=x3+ax2+bx-1-a-b
=(x-1)[x2+(a+1)x+a+b+1]
从而另两个零点为方程x2+(a+1)x+a+b+1=0的两根,且一根大于1,一根小于1而大于零,设g(x)=x2+(a+1)x+a+b+1,

而![]() 表示可行
表示可行![]() 域中的点(a,b)与原点连线的斜率k,直线OA的斜率k1=-
域中的点(a,b)与原点连线的斜率k,直线OA的斜率k1=-![]() ,直线2a+b+
,直线2a+b+![]() 3=0的斜率k2=-2,所以k∈(-2,-
3=0的斜率k2=-2,所以k∈(-2,-![]() ),即
),即![]() ∈(-2,-
∈(-2,-![]() ).
).

练习册系列答案
相关题目
 的一个零点为
的一个零点为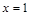 ,另外两个零点可分别作为一个椭圆、一双曲线的离心率,则
,另外两个零点可分别作为一个椭圆、一双曲线的离心率,则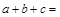 ;
; 的取值范围是
.
的取值范围是
. 的一个零点为
的一个零点为 ,另外两个零点分别可作为椭圆和双曲线的离心率,则
,另外两个零点分别可作为椭圆和双曲线的离心率,则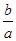 的取值范围是______.
的取值范围是______. 的一个零点为
的一个零点为 ,另外两个零点分别可作为椭圆和双曲线的离心率,则
,另外两个零点分别可作为椭圆和双曲线的离心率,则 的取值范围是______.
的取值范围是______.