题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c.若asinBcosC+csinBcosA=
b,且a>b,则∠B等于( )
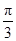b,且a>b,则∠B等于( )A． | B． | C． | D． |
A
由asiBcosC+csinBcosA=b得
sinAsinBcosC+sinCsinBcosA=sinB,
因为sinB≠0,
所以sinAcosC+cosAsinC=,
即sin(A+C)=,sinB=,
又a>b,则∠B=,故选A.
b得sinAsinBcosC+sinCsinBcosA=
sinB,因为sinB≠0,
所以sinAcosC+cosAsinC=
,即sin(A+C)=
,sinB=,又a>b,则∠B=
,故选A.
练习册系列答案
相关题目
，
，
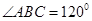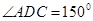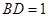（千米），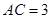
（千米）．假设小王和小李徒步攀登的速度为每小时1200米，请问：两位登山爱好者能否在2个小时内徒步登上山峰．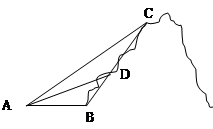
中，已知
，又
的面积等于6.
的三边之长；
是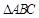
（含边界）内一点，
的距离分别为
，求
的取值范围.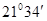
,小王想在某住宅小区买房，该小区的楼高7层，每层3m，楼与楼间相距15m，要使所买楼房在一年四季正午的太阳不被前面的楼房遮挡，应该选购该楼的最低层数是（ ）
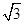－1)海里的C处的缉私船奉命以10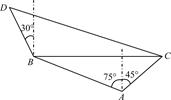
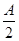，当A取A0时，f(A)取极大值f(A0)，试求A0和f(A0)的值；
·
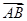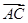＝－1，求BC边长的最小值．
.
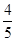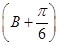的值；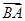
·
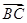＝20，求△ABC的面积．
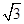，则C＝________，sin A＝________.
中，已知
，则
.