题目内容
三角形的面积为S=
(a+b+c)r，a、b、c为三角形的边长，r为三角形内切圆的半径，利用类比推理可以得出四面体的体积为______．
| 1 |
| 2 |
设四面体的内切球的球心为O，则球心O到四个面的距离都是r，
根据三角形的面积的求解方法：分割法，将O与四顶点连起来，可得四面体的体积等于以O为顶点，分别以四个面为底面的4个三棱锥体积的和，
∴V=
（S1+S2+S3+S4）r，
故答案为：V=
（S1+S2+S3+S4）r．
根据三角形的面积的求解方法：分割法，将O与四顶点连起来，可得四面体的体积等于以O为顶点，分别以四个面为底面的4个三棱锥体积的和，
∴V=
| 1 |
| 3 |
故答案为：V=
| 1 |
| 3 |
练习册系列答案
相关题目
．
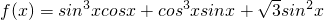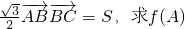的取值范围．
（a+b+c）r（r为三角形内切圆半径）。