题目内容
【题目】已知曲线C:y=![]() ,D为直线y=
,D为直线y=![]() 上的动点,过D作C的两条切线,切点分别为A,B.
上的动点,过D作C的两条切线,切点分别为A,B.
(1)证明:直线AB过定点:
(2)若以E(0,![]() )为圆心的圆与直线AB相切,且切点为线段AB的中点,求四边形ADBE的面积.
)为圆心的圆与直线AB相切,且切点为线段AB的中点,求四边形ADBE的面积.
【答案】(1)见详解;(2) 3或![]() .
.
【解析】
可用解析法和几何法证明。解析法可设A,B两点的坐标分别为![]() ,
,![]() ,然后求出A,B两点处的切线,两条切线交于直线
,然后求出A,B两点处的切线,两条切线交于直线![]() 之上,所以交点的纵坐标为
之上,所以交点的纵坐标为![]()
联立方程可解![]() 和
和![]() 的关系。之后用两点式求出直线
的关系。之后用两点式求出直线![]() 方程,最后根据直线
方程,最后根据直线![]() 方程求出它所过的定点.(2)应用四边形面积公式,代入化简出关于
方程求出它所过的定点.(2)应用四边形面积公式,代入化简出关于![]() 和
和![]() 的对称式。然后分情况讨论求解。如果不知道四面下面积公式则可以将四边形分成两个三角形求面积之后做和,但会稍微麻烦一些。(此题若用向量积的概念则更为容易)
的对称式。然后分情况讨论求解。如果不知道四面下面积公式则可以将四边形分成两个三角形求面积之后做和,但会稍微麻烦一些。(此题若用向量积的概念则更为容易)
(1)证明:设A,B两点的坐标分别为![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
则切线DA为:![]() ---------①,切线DB为:
---------①,切线DB为:![]() --------②,
--------②,
代入![]() 得
得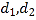 ,
,![]() 得
得![]() ,因为
,因为![]() 故消去得交点的纵坐标
故消去得交点的纵坐标![]() ,
,
因为DA和DB的交点D为直线![]() 上的动点,所以有
上的动点,所以有![]() ,
,![]() ,
,
直线AB为![]() ,点A,B在曲线
,点A,B在曲线![]() 上,则有
上,则有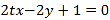 ,整理得
,整理得![]() ,即
,即![]() .当
.当![]() ,
,![]() 时无论
时无论![]() ,
,![]() 取何值时,此等式均成立。因此直线AB过定点
取何值时,此等式均成立。因此直线AB过定点![]() ,得证。
,得证。
(2)设AB的中点为G,由题得G点坐标为![]() ,则
,则![]() ,又
,又![]() .由题意知
.由题意知![]() ,即
,即![]() 即
即![]() .代入
.代入![]() 得
得![]() 整理得
整理得![]() .
.
因![]() ,故
,故![]() .所以
.所以![]() 或
或![]() .
.
由第一问中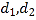 ,为这里的
,为这里的![]() 为D点坐标,然而
为D点坐标,然而![]() ,故
,故
![]() ,所以
,所以![]() ,又因为
,又因为![]() .所以
.所以![]() 。即D坐标为
。即D坐标为![]() .
.
那么![]() ,
,![]() .
.
设![]() 为
为![]() 与
与![]() 的夹角,那么有
的夹角,那么有
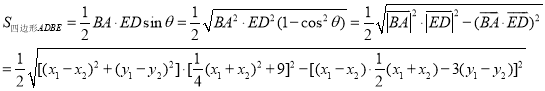
代入![]() 进行化简有
进行化简有![]()
若![]() ,则
,则![]() .
.
若![]() ,则
,则![]() ,
,![]()
代入有![]() .
.
所以四边形ADBE的面积为3或![]() .
.

练习册系列答案
相关题目