题目内容
【题目】对于数列![]() ,称
,称![]() (其中
(其中![]() )为数列
)为数列![]() 的前k项“波动均值”.若对任意的
的前k项“波动均值”.若对任意的![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为“趋稳数列”.
为“趋稳数列”.
(1)若数列1,![]() ,2为“趋稳数列”,求
,2为“趋稳数列”,求![]() 的取值范围;
的取值范围;
(2)若各项均为正数的等比数列![]() 的公比
的公比![]() ,求证:
,求证:![]() 是“趋稳数列”;
是“趋稳数列”;
(3)已知数列![]() 的首项为1,各项均为整数,前
的首项为1,各项均为整数,前![]() 项的和为
项的和为![]() . 且对任意
. 且对任意![]() ,都有
,都有![]() , 试计算:
, 试计算:![]() (
(![]() ).
).
【答案】(1)![]() (2)证明见解析,(3)
(2)证明见解析,(3)![]()
【解析】
(1)由新定义可得![]() ,解不等式可得
,解不等式可得![]() 的范围;(2)运用等比数列的通项公式和求和公式,结合新定义,运用不等式的性质即可得证;(3)由任意
的范围;(2)运用等比数列的通项公式和求和公式,结合新定义,运用不等式的性质即可得证;(3)由任意![]() ,
,![]() ,都有
,都有![]() ,可得
,可得![]() ,由等比数列的通项公式,可得
,由等比数列的通项公式,可得![]() ,结合新定义和二项式定理,化简整理即可得到所求值.
,结合新定义和二项式定理,化简整理即可得到所求值.
(1)由题意![]() ,即
,即![]() ,
,
解得![]() ,
,
(2)由已知,设![]() ,因
,因![]() 且
且![]() ,故对任意的
,故对任意的![]() ,都有
,都有![]() ,
,
∴![]()
![]()
![]() ,
,
因![]() ∴
∴![]()
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
∴![]()
即对任意的![]() ,都有
,都有![]() ,故
,故![]() 是“趋稳数列”,
是“趋稳数列”,
(3) 当![]() 时,
时,![]()
当![]() 时,
时,![]()
∴![]()
同理,![]() ,
,
因![]()
∴![]()
![]()
即![]() ,
,
所以![]() 或
或 ![]()
所以 ![]() 或
或 ![]()
因为![]() ,且
,且![]() ,所以
,所以![]() , 从而
, 从而![]() ,
,
所以![]()
![]()
![]()
![]() .
.

练习册系列答案
相关题目
【题目】近来天气变化无常,陡然升温、降温幅度大于![]() 的天气现象出现增多.陡然降温幅度大于
的天气现象出现增多.陡然降温幅度大于![]() 容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的
容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的![]() 名幼儿进行调查,得到了如下的列联表,若在全部
名幼儿进行调查,得到了如下的列联表,若在全部![]() 名幼儿中随机抽取
名幼儿中随机抽取![]() 人,抽到患伤风感冒疾病的幼儿的概率为
人,抽到患伤风感冒疾病的幼儿的概率为![]() ,
,
(1)请将下面的列联表补充完整;
患伤风感冒疾病 | 不患伤风感冒疾病 | 合计 | |
男 | 25 | ||
女 | 20 | ||
合计 | 100 |
(2)能否在犯错误的概率不超过![]() 的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
(3)已知在患伤风感冒疾病的![]() 名女性幼儿中,有
名女性幼儿中,有![]() 名又患黄痘病.现在从患伤风感冒疾病的
名又患黄痘病.现在从患伤风感冒疾病的![]() 名女性中,选出
名女性中,选出![]() 名进行其他方面的排查,记选出患黄痘病的女性人数为
名进行其他方面的排查,记选出患黄痘病的女性人数为![]() ,求
,求![]() 的分布列以及数学期望.下面的临界值表供参考:
的分布列以及数学期望.下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: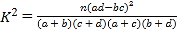 ,其中
,其中![]()